【题目】在平面直角坐标系![]() 中,点
中,点![]() ,若射线
,若射线![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为腰的等腰三角形,就称点
为腰的等腰三角形,就称点![]() 为线段
为线段![]() 关于射线
关于射线![]() 的等腰点.
的等腰点.
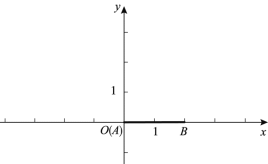
(1)如图, ![]() ,
,
①若![]() ,则线段
,则线段![]() 关于射线
关于射线![]() 的等腰点的坐标是_____;
的等腰点的坐标是_____;
②若![]() ,且线段
,且线段![]() 关于射线
关于射线![]() 的等腰点的纵坐标小于1,求
的等腰点的纵坐标小于1,求![]() 的取值范围;
的取值范围;
(2) 若![]() ,且射线
,且射线![]() 上只存在一个线段
上只存在一个线段![]() 关于射线
关于射线![]() 的等腰点,则
的等腰点,则![]() 的取值范围是__________.
的取值范围是__________.
参考答案:
【答案】(1)(0,2);(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
(1)①根据线段AB关于射线OC的等腰点的定义可知OP=AB=2,即可解答;
②如图,设以点![]() 为圆心,
为圆心, ![]() 为半径的圆与直线
为半径的圆与直线![]() 在第二象限的交点为
在第二象限的交点为![]() ,作
,作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,C位于D点左侧时满足条件;
,C位于D点左侧时满足条件;
(2)如图,作CH⊥y轴于H.分别以A,B为圆心,AB为半径作⊙A,⊙B,先求出∠COH=30°,由射线OC上只存在一个线段AB关于射线OC的等腰点,推出射线OC与⊙A,⊙B只有一个交点,然后讨论几种特殊情况即可找到范围.
解:(1)①如图1中,由题意可知A(0,0),B(2,0),C(0,1),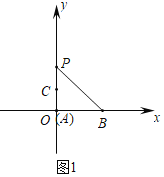
∵点P是线段AB关于射线OC的等腰点,
∴OP=AB=2,
∴P(0,2);
②如图,设以点![]() 为圆心,
为圆心, ![]() 为半径的圆与直线
为半径的圆与直线![]() 在第二象限的交点为
在第二象限的交点为![]() ,作
,作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,
,
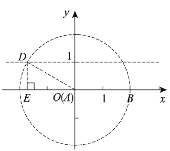
![]() ,
,
在![]() 中,根据勾股定理得
中,根据勾股定理得![]() ,
,
![]() 的取值范围是
的取值范围是![]() ;
;
(2)如下图,作CH⊥y轴于H.分别以A,B为圆心,AB为半径作⊙A,⊙B.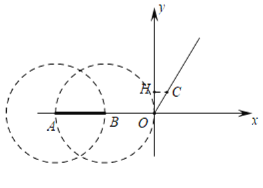
由题意C(![]() ,1),
,1),
∴CH=![]() ,OH=1,
,OH=1,
∴tan∠COH![]() ,
,
∴∠COH=30°,
当⊙B经过原点时,B(-2,0),此时t=-4,
∵射线OC上只存在一个线段AB关于射线OC的等腰点,
∴射线OC与⊙A,⊙B只有一个交点,观察图象可知当-4<t≤-2时,满足条件,
如下图,当点A在原点时,∵∠POB=60°,此时两圆的交点P在射线OC上,满足条件,此时t=0,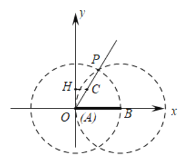
如下图,当⊙B与OC相切于P时,连接BP,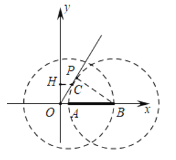
∴OC是⊙B的切线,
∴OP⊥BP,
∴∠OPB=90°,
∵BP=2,∠POB=60°,
∴![]() ,
,
∴![]() ,此时
,此时![]() ,
,
如下图,当⊙A与OC相切时,同法可得![]() ,此时
,此时![]() ,
,
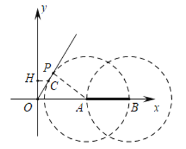
观察图形可知,满足条件的t的值为![]() ,
,
综上所述,满足条件t的值为![]() 或
或![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,直线
中,直线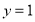 与一次函数
与一次函数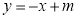 的图象交于点
的图象交于点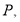 与反比例函数
与反比例函数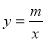 的图象交于点
的图象交于点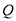 ,点
,点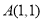 与点
与点 关于
关于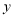 轴对称.
轴对称.(1)直接写出点
 的坐标;
的坐标;(2)求点
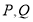 的坐标(用含
的坐标(用含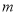 的式子表示);
的式子表示);(3)若
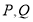 两点中只有一个点在线段
两点中只有一个点在线段 上,直接写出
上,直接写出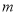 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
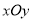 中,抛物线
中,抛物线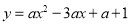 与
与 轴交于点
轴交于点 .
.(1)求点
 的坐标(用含
的坐标(用含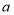 的式子表示);
的式子表示);(2)求抛物线的对称轴;
(3)已知点
 .若抛物线与线段
.若抛物线与线段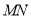 恰有一个公共点,结合函数图象,求
恰有一个公共点,结合函数图象,求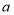 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形
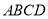 是正方形,将线段
是正方形,将线段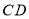 绕点
绕点 逆时针旋转
逆时针旋转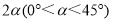 ,得到线段
,得到线段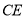 ,连接
,连接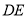 ,过点
,过点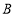 作
作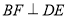 交
交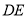 的延长线于
的延长线于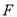 ,连接
,连接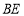 .
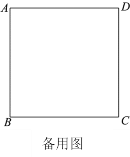
.(1)依题意补全图1;
(2)直接写出
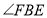 的度数;
的度数;(3)连接
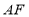 ,用等式表示线段
,用等式表示线段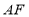 与
与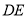 的数量关系,并证明.
的数量关系,并证明.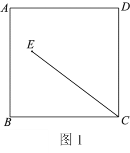
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的布袋中装有标着数字2,3,4,5的4个小球,这4个小球的材质、大小和形状完全相同,现从中随机摸出两个小球,这两个小球上的数字之积大于9的概率为( )
A.
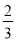 B.
B.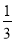 C.
C.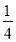 D.
D.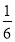
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x
…
﹣2
﹣1
0
1
2
…
y
…
0
4
6
6
4
…
从上表可知,下列说法中,错误的是( )
A. 抛物线于x轴的一个交点坐标为(﹣2,0)
B. 抛物线与y轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
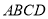 中,
中,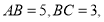 点
点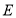 为射线
为射线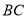 上一动点,将
上一动点,将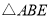 沿
沿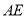 折叠,得到
折叠,得到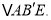 若
若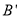 恰好落在射线
恰好落在射线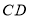 上,则
上,则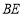 的长为________.
的长为________.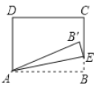
相关试题

