【题目】四边形![]() 是正方形,将线段
是正方形,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到线段
,得到线段![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,连接
,连接![]() .
.
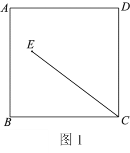
(1)依题意补全图1;
(2)直接写出![]() 的度数;
的度数;
(3)连接![]() ,用等式表示线段
,用等式表示线段![]() 与
与![]() 的数量关系,并证明.
的数量关系,并证明.
参考答案:
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() ,理由见解析
,理由见解析
【解析】
(1)按照题中的表述画出图形即可;
(2)由题意可知,CD=CE=CB,∠ECD=2α,∠ABC=∠BCD=∠CDA=∠DAB=90°,根据题中角度关系推理即可;
(3)作AH⊥AF,交BF的延长线于点H,先通过条件证明△HAB≌△FAD,可得HB=FD,AH=AF,HF=DE,∠H=45°,从而知道HF与AF的数量关系,即可得线段AF与DE的数量关系.
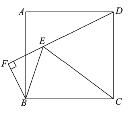
解:(1)补全图形,如图所示.
(2)![]() ,
,
设DF与AB交于点G,如图所示:
由题意得,CD=CE=CB,∠ECD=2α,∠ABC=∠BCD=∠CDA=∠DAB=90°,
∴∠EDC=90°-α,∠BCE=90°-2α,
∴∠CBE=45°+α,∠ADF=α,
∴∠ABE=45°-α.
∵BF⊥DE,
∴∠BFD=90°.
∵∠AGD=∠FGB,
∴∠FBG=α
∴∠FBE=∠FEB=45°;
(3)![]() .
.
证明:如图,作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,设
,设![]() 与
与![]() 交于点
交于点![]() ,
,
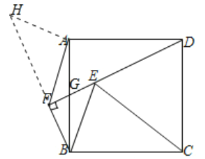
根据题意可知,![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数
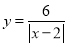 的图象与性质并解决问题.
的图象与性质并解决问题.小明根据学习函数的经验,对问题进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数
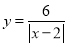 的自变量
的自变量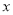 的取值范围是 ;
的取值范围是 ;(2)取几组
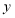 与
与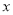 的对应值,填写在下表中.
的对应值,填写在下表中.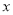
…

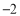
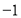
0
1
1.2
1.25
2.75
2.8
3
4
5
6
8
…
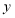
…
1
1.5
2
3
6
7.5
8
8
7.5
6
3
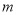
1.5
1
…
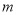 的值为_____________;
的值为_____________;(3)如下图,在平面直角坐标系
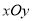 中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;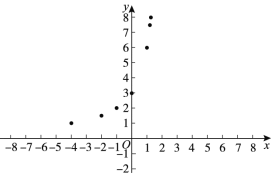
(4)获得性质,解决问题:
①通过观察、分析、证明,可知函数
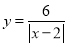 的图象是轴对称图形,它的对称轴是____________;
的图象是轴对称图形,它的对称轴是____________;②过点
 作直线
作直线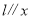 轴,与函数
轴,与函数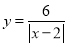 的图象交于点
的图象交于点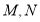 (点
(点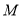 在点
在点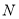 的左侧),则
的左侧),则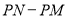 的值为____________.
的值为____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
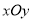 中,直线
中,直线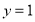 与一次函数
与一次函数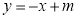 的图象交于点
的图象交于点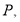 与反比例函数
与反比例函数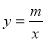 的图象交于点
的图象交于点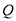 ,点
,点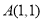 与点
与点 关于
关于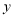 轴对称.
轴对称.(1)直接写出点
 的坐标;
的坐标;(2)求点
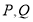 的坐标(用含
的坐标(用含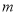 的式子表示);
的式子表示);(3)若
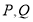 两点中只有一个点在线段
两点中只有一个点在线段 上,直接写出
上,直接写出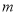 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
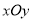 中,抛物线
中,抛物线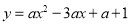 与
与 轴交于点
轴交于点 .
.(1)求点
 的坐标(用含
的坐标(用含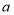 的式子表示);
的式子表示);(2)求抛物线的对称轴;
(3)已知点
 .若抛物线与线段
.若抛物线与线段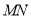 恰有一个公共点,结合函数图象,求
恰有一个公共点,结合函数图象,求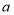 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
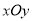 中,点
中,点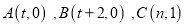 ,若射线
,若射线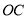 上存在点
上存在点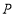 ,使得
,使得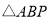 是以
是以 为腰的等腰三角形,就称点
为腰的等腰三角形,就称点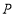 为线段
为线段 关于射线
关于射线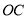 的等腰点.
的等腰点.(1)如图,
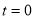 ,
,①若
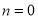 ,则线段
,则线段 关于射线
关于射线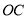 的等腰点的坐标是_____;
的等腰点的坐标是_____;②若
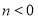 ,且线段
,且线段 关于射线
关于射线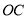 的等腰点的纵坐标小于1,求
的等腰点的纵坐标小于1,求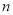 的取值范围;
的取值范围;(2) 若
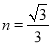 ,且射线
,且射线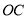 上只存在一个线段
上只存在一个线段 关于射线
关于射线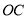 的等腰点,则
的等腰点,则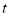 的取值范围是__________.
的取值范围是__________.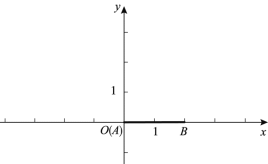
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的布袋中装有标着数字2,3,4,5的4个小球,这4个小球的材质、大小和形状完全相同,现从中随机摸出两个小球,这两个小球上的数字之积大于9的概率为( )
A.
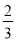 B.
B.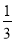 C.
C.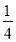 D.
D.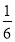
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x
…
﹣2
﹣1
0
1
2
…
y
…
0
4
6
6
4
…
从上表可知,下列说法中,错误的是( )
A. 抛物线于x轴的一个交点坐标为(﹣2,0)
B. 抛物线与y轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的
相关试题

