【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() 的坐标(用含
的坐标(用含![]() 的式子表示);
的式子表示);
(2)求抛物线的对称轴;
(3)已知点![]() .若抛物线与线段
.若抛物线与线段![]() 恰有一个公共点,结合函数图象,求
恰有一个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 的取值范围是
的取值范围是![]()
【解析】
(1)与![]() 轴的交点横坐标为0,然后计算
轴的交点横坐标为0,然后计算![]() 时的函数值即可求出坐标;
时的函数值即可求出坐标;
(2)根据抛物线的对称轴为![]() 求解即可;
求解即可;
(3)由N点和A点的坐标,可知点A在点N的上方,令抛物线上的点![]() ,可得
,可得![]() ,分a>0,a<0两种情形分别求解即可解决问题.
,分a>0,a<0两种情形分别求解即可解决问题.
解:(1)∵抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
令![]() ,得
,得![]() .
.
![]() .
.
(2)由抛物线![]() 可知
可知![]() .
.
∴抛物线的对称轴为直线![]() .
.
(3)对于任意的实数![]() ,都有
,都有![]() .
.
可知点![]() 总在点
总在点![]() 的上方.
的上方.
令抛物线上的点![]() .
.
![]() .
.
①如图1,当![]() 时,
时, ![]() .
.
∴点![]() 在点
在点![]() 的上方.
的上方.
结合函数图象,可知抛物线与线段![]() 没有公共点.
没有公共点.

②当![]() 时
时
(i)如图2,当抛物线经过点![]() 时,
时, ![]() .
.
![]() .
.
结合函数图象,可知抛物线与线段![]() 恰有一个公共点
恰有一个公共点![]() .
.

(ii)当![]() 时,可知抛物线与线段
时,可知抛物线与线段![]() 没有公共点.
没有公共点.
(ⅲ)如图3,当![]() ,时,
,时, ![]() .
.
∴点![]() 在点
在点![]() 的下方.
的下方.
结合函数图象,可知抛物线与线段![]() 恰有一个公共点.
恰有一个公共点.
综上所述, ![]() 的取值范围是
的取值范围是![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 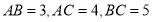 .在同一平面内,
.在同一平面内, 内部一点
内部一点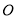 到
到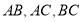 的距离都等于
的距离都等于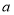 (
(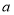 为常数),到点
为常数),到点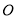 的距离等于
的距离等于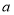 的所有点组成图形
的所有点组成图形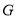 .
.(1)直接写出
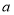 的值;
的值;(2)连接
 并延长,交
并延长,交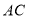 于点
于点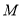 ,过点
,过点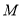 作
作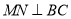 于点
于点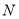 .
.①求证:
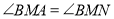 ;
;②求直线
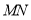 与图形
与图形 的公共点个数.
的公共点个数.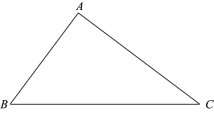
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数
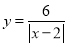 的图象与性质并解决问题.
的图象与性质并解决问题.小明根据学习函数的经验,对问题进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数
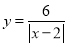 的自变量
的自变量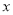 的取值范围是 ;
的取值范围是 ;(2)取几组
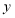 与
与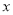 的对应值,填写在下表中.
的对应值,填写在下表中.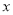
…

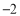
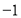
0
1
1.2
1.25
2.75
2.8
3
4
5
6
8
…
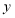
…
1
1.5
2
3
6
7.5
8
8
7.5
6
3
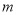
1.5
1
…
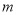 的值为_____________;
的值为_____________;(3)如下图,在平面直角坐标系
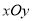 中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;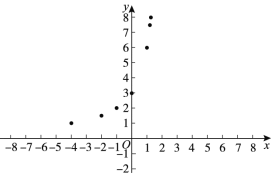
(4)获得性质,解决问题:
①通过观察、分析、证明,可知函数
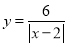 的图象是轴对称图形,它的对称轴是____________;
的图象是轴对称图形,它的对称轴是____________;②过点
 作直线
作直线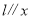 轴,与函数
轴,与函数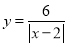 的图象交于点
的图象交于点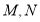 (点
(点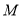 在点
在点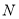 的左侧),则
的左侧),则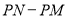 的值为____________.
的值为____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
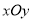 中,直线
中,直线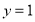 与一次函数
与一次函数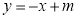 的图象交于点
的图象交于点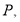 与反比例函数
与反比例函数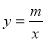 的图象交于点
的图象交于点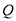 ,点
,点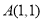 与点
与点 关于
关于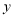 轴对称.
轴对称.(1)直接写出点
 的坐标;
的坐标;(2)求点
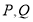 的坐标(用含
的坐标(用含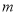 的式子表示);
的式子表示);(3)若
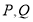 两点中只有一个点在线段
两点中只有一个点在线段 上,直接写出
上,直接写出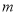 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形
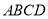 是正方形,将线段
是正方形,将线段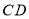 绕点
绕点 逆时针旋转
逆时针旋转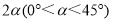 ,得到线段
,得到线段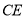 ,连接
,连接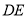 ,过点
,过点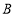 作
作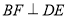 交
交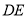 的延长线于
的延长线于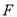 ,连接
,连接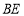 .
.(1)依题意补全图1;
(2)直接写出
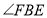 的度数;
的度数;(3)连接
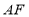 ,用等式表示线段
,用等式表示线段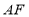 与
与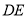 的数量关系,并证明.
的数量关系,并证明.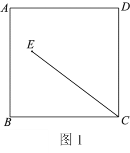
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
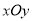 中,点
中,点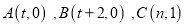 ,若射线
,若射线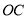 上存在点
上存在点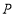 ,使得
,使得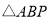 是以
是以 为腰的等腰三角形,就称点
为腰的等腰三角形,就称点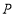 为线段
为线段 关于射线
关于射线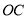 的等腰点.
的等腰点.(1)如图,
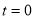 ,
,①若
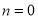 ,则线段
,则线段 关于射线
关于射线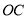 的等腰点的坐标是_____;
的等腰点的坐标是_____;②若
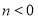 ,且线段
,且线段 关于射线
关于射线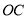 的等腰点的纵坐标小于1,求
的等腰点的纵坐标小于1,求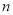 的取值范围;
的取值范围;(2) 若
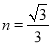 ,且射线
,且射线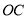 上只存在一个线段
上只存在一个线段 关于射线
关于射线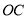 的等腰点,则
的等腰点,则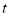 的取值范围是__________.
的取值范围是__________.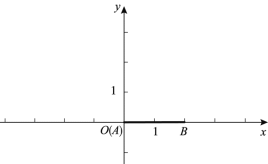
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的布袋中装有标着数字2,3,4,5的4个小球,这4个小球的材质、大小和形状完全相同,现从中随机摸出两个小球,这两个小球上的数字之积大于9的概率为( )
A.
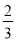 B.
B.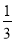 C.
C.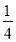 D.
D.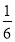
相关试题

