【题目】在如图所示的网格中,每个小正方形的边长都为1.
(1)试作出直角坐标系,使点A的坐标为(2,-1);
(2)在(1)中建立的直角坐标系中描出点B(3,4),C(0,1),并求三角形ABC的面积.
参考答案:
【答案】(1)答案见解析;(2)6
【解析】试题分析:(1)根据点A的坐标,向左平移2个单位,向上平移1个单位,确定出坐标原点的位置,然后以水平方向为x轴,竖直方向为y轴,建立平面直角坐标系即可;
(2)根据网格结构的特点以及平面直角坐标系找出点B、C的位置,然后顺次连接得到△ABC;利用△ABC所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得到△ABC的面积.
试题解析:(1)如图所示:
(2)如图.
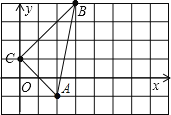
S三角形ABC=3×5-![]() ×3×3-
×3×3-![]() ×2×2-
×2×2-![]() ×5×1=15-
×5×1=15-![]() -2-
-2-![]() =6.
=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于0,1以及真分数p,q,r,若p<q<r,我们称q为p和r的中间分数.为了帮助我们找中间分数,制作了下表:
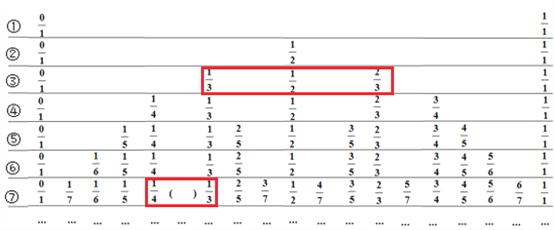
两个不等的正分数有无数多个中间分数.例如:上表中第③行中的3个分数
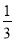 、
、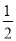 、
、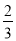 ,有
,有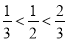 ,所以
,所以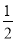 为
为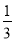 和
和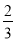 的一个中间分数,在表中还可以找到
的一个中间分数,在表中还可以找到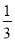 和
和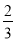 的中间分数
的中间分数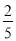 ,
, 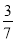 ,
, 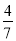 ,
, 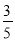 .把这个表一直写下去,可以找到
.把这个表一直写下去,可以找到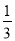 和
和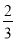 更多的中间分数.
更多的中间分数.(1)按上表的排列规律,完成下面的填空:
①上表中括号内应填的数为 ;
②如果把上面的表一直写下去,那么表中第一个出现的
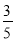 和
和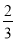 的中间分数是 ;
的中间分数是 ;(2)写出分数
 和
和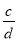 (a、b、c、d均为正整数,
(a、b、c、d均为正整数,  ,
, 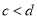 )的一个中间分数(用含a、b、c、d的式子表示),并证明;
)的一个中间分数(用含a、b、c、d的式子表示),并证明;(3)若
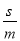 与
与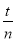 (m、n、s、 t均为正整数)都是
(m、n、s、 t均为正整数)都是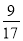 和
和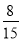 的中间分数,则
的中间分数,则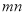 的最小值为 .
的最小值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥DE,求证:∠D+∠BCD-∠B=180°.
证明:过点C作CF∥AB.
∵AB∥CF(已知),
∴∠B=________(____________________).
∵AB∥DE,CF∥AB(已知),
∴CF∥DE(__________________________________).
∴∠2+________=180°(________________________).
∵∠2=∠BCD-________(已知),
∴∠D+∠BCD-∠B=180°(等量代换).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于底面上一点).已知E、F在AB边上,是被剪去一个等腰直角三角形斜边的两个端点,设AE=BF=xcm.
(1)若折成的包装盒恰好是正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?
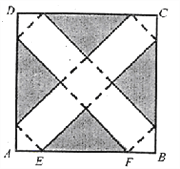
-
科目: 来源: 题型:
查看答案和解析>>【题目】资料:小球沿直线撞击水平格档反弹时(不考虑垂直撞击),撞击路线与水平格档所成的锐角等于反弹路线与水平格档所成的锐角.以图(1)为例,如果黑球
 沿从
沿从 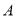 到
到 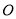 方向在
方向在  点处撞击
点处撞击  边后将沿从
边后将沿从 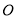 到
到 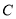 方向反弹,根据反弹原则可知
方向反弹,根据反弹原则可知 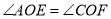 ,即
,即 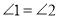 .如图(2)和(3),
.如图(2)和(3), 是一个长方形的弹子球台面,有黑白两球
是一个长方形的弹子球台面,有黑白两球 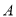 和
和 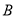 ,小球沿直线撞击各边反弹时遵循资料中的反弹原则.(回答以下问题时将黑白两球均看作几何图形中的点,不考虑其半径大小)
,小球沿直线撞击各边反弹时遵循资料中的反弹原则.(回答以下问题时将黑白两球均看作几何图形中的点,不考虑其半径大小)
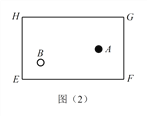
(1)探究(1):黑球
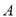 沿直线撞击台边
沿直线撞击台边  哪一点时,可以使黑球
哪一点时,可以使黑球  经台边
经台边 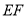 反弹一次后撞击到白球
反弹一次后撞击到白球  ?请在图(2)中画出黑球
?请在图(2)中画出黑球 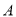 的路线图,标出撞击点,并简单证明所作路线是否符合反弹原则.
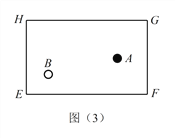
的路线图,标出撞击点,并简单证明所作路线是否符合反弹原则.(2)探究(2):黑球
 沿直线撞击台边
沿直线撞击台边 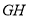 哪一点时,可以使黑球
哪一点时,可以使黑球  先撞击台边
先撞击台边  反弹一次后,再撞击台边
反弹一次后,再撞击台边  反弹一次撞击到白球
反弹一次撞击到白球  ?请在图(3)中画出黑球
?请在图(3)中画出黑球  的路线图,标出黑球撞击
的路线图,标出黑球撞击  边的撞击点,简单说明作法,不用证明.
边的撞击点,简单说明作法,不用证明. -
科目: 来源: 题型:
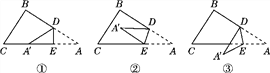
查看答案和解析>>【题目】△ABC是一个三角形的纸片,点D,E分别是△ABC边AB,AC上的两点.
(1)如图①,如果沿直线DE折叠,则∠BDA′与∠A的关系是____________;
(2)如果折成图②的形状,猜想∠BDA′,∠CEA′和∠A的关系,并说明理由;
(3)如果折成图③的形状,猜想∠BDA′,∠CEA′和∠A的关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+
 =0,过C作CB⊥x轴于B.
=0,过C作CB⊥x轴于B.
(1)求三角形ABC的面积;
(2)如图②,若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;
(3)在y轴上是否存在点P,使得三角形ACP和三角形ABC的面积相等?若存在,求出P点的坐标;若不存在,请说明理由.
相关试题

