【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点D在AB上,AD=AC,AF⊥CD交CD于点E,交CB于点F,则CF的长是________________.

参考答案:
【答案】1.5
【解析】
连接DF,由勾股定理求出AB=5,由等腰三角形的性质得出∠CAF =∠DAF,由SAS证明△ADF≌△ACF,得出CF=DF,∠ADF=∠ACF=∠BDF=90°,设CF=DF=x,则BF=4-x,在Rt△BDF中,由勾股定理得出方程,解方程即可.
连接DF,如图所示:
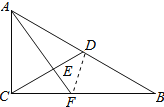
在Rt△ABC中,∠ACB=90°,AC=3,BC=4,由勾股定理求得AB=5,
∵AD=AC=3,AF⊥CD,
∴∠CAF =∠DAF,BD=AB-AD=2,
在△ADF和△ACF中,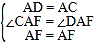
∴△ADF≌△ACF(SAS),
∴∠ADF=∠ACF=90°,CF=DF,
∴∠BDF=90°,
设CF=DF=x,则BF=4-x,
在Rt△BDF中,由勾股定理得:DF2+BD2=BF2,
即x2+22=(4-x)2,
解得:x=1.5;
∴CF=1.5;
故答案为:1.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.
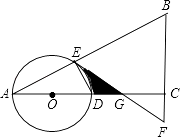
(1)试判断直线EF与⊙O的位置关系,并说明理由;
(2)若OA=2,∠A=30°,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1) ;
;
(2) .
.
(1)tan60°﹣|﹣2|+
(2)(1+ )÷
)÷  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天时间.
(1)轮船到达目的地开始卸货,平均卸货速度v(单位:吨/天)与卸货天数t之间有怎样的函数关系?
(2)由于遇到紧急情况,要求船上货物不超过5天卸货完毕,那么平均每天至少要缷货多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
, ,
, 试说明直线AD与BC垂直
试说明直线AD与BC垂直 请在下面的解答过程的空格内填空或在括号内填写理由
请在下面的解答过程的空格内填空或在括号内填写理由 .
.
理由:
 ,
, 已知
已知
 ______
______ ______,
______, ______
______
 ______
______ ______
______
又
 ,
, 已知
已知
 ______
______ 等量代换
等量代换
 ______
______ ______,
______, ______
______
 ______
______
 ,
, 已知
已知
 ,
, ,
, ______
______ ______.
______. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上A,B两点对应的数分别为a和b,且a,b满足等式
 ,p为数轴上一动点,对应的数为x.
,p为数轴上一动点,对应的数为x. ______,
______,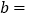 ______,线段
______,线段 ______.
______. 数轴上是否存在点p,使
数轴上是否存在点p,使 ?若存在,求出x的值;若不存在,请说明理由.
?若存在,求出x的值;若不存在,请说明理由. 在
在 的条件下,若M,N分别是线段AB,PB的中点,试求线段MN的长.
的条件下,若M,N分别是线段AB,PB的中点,试求线段MN的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司组织员工到附近的景点旅游,根据旅行社提供的收费方案,绘制了如图所示的图象,图中折线ABCD表示人均收费y(元)与参加旅游的人数x(人)之间的函数关系.

(1)当参加旅游的人数不超过10人时,人均收费为元;
(2)如果该公司支付给旅行社3600元,那么参加这次旅游的人数是多少?
相关试题

