【题目】如图,已知在正方形ABCD中,AE∥BD,BE=BD,BE交AD于F.求证:DE=DF.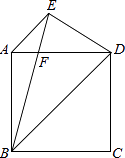
参考答案:
【答案】证明:连接AC,交BD于点O,作EG⊥BD于点G.
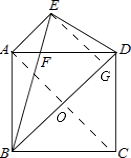
∵四边形ABCD是正方形,
∴AC⊥BD,
∵AE∥BD,
∴四边形AOGE是矩形,
∴EG=AO= ![]() AC=
AC= ![]() BD=
BD= ![]() BE,
BE,
∴∠EBD=30°,
∵∠EBD=30°,BE=BD,
∴∠BED=75°,
∵∠EFD=∠FDB+∠EBD=45+30=75°,
∴∠DEF=∠DFE,
∴DF=DE.
【解析】连接AC,交BD于点O,作EG⊥BD垂足为G,先证明四边形AOGE是矩形,从而可得到EG=![]() BD=
BD=![]() BE,从而可求得∠EBD=30°,接下来可求得∠BED=75°,然后再依据∠EFD=∠FDB+∠EBD求得∠EFD的度数,故∠DEF=∠DFE,最后,依据等边对等角的性质进行证明即可.
BE,从而可求得∠EBD=30°,接下来可求得∠BED=75°,然后再依据∠EFD=∠FDB+∠EBD求得∠EFD的度数,故∠DEF=∠DFE,最后,依据等边对等角的性质进行证明即可.
【考点精析】本题主要考查了等腰三角形的性质和含30度角的直角三角形的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半才能正确解答此题.
-
科目: 来源: 题型:
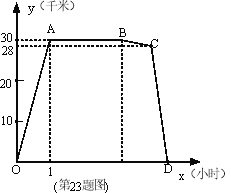
查看答案和解析>>【题目】(2011福建龙岩,23, 12分) 周六上午8:00小明从家出发,乘车1小时到郊外某基地参加社会实践活动,在基地活动2.2小时后,因家里有急事,他立即按原路以4千米/时的平均速度步行返回.同时爸爸开车从家出发沿同一路线接他,在离家28千米处与小明相遇。接到小明后保持车速不变,立即按原路返回.设小明离开家的时间为x小时,小名离家的路程y (干米) 与x (小时)之间的函致图象如图所示,
(1)小明去基地乘车的平均速度是________千米/小时,爸爸开车的平均速度应是________千米/小时;
(2)求线段CD所表示的函敛关系式;
(3)问小明能否在12:0 0前回到家?若能,请说明理由:若不能,请算出12:00时他离家的路程,
-
科目: 来源: 题型:
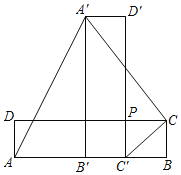
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=a,BC=b(a>2b),点P在边CD上,且PC=BC,长方形ABCD绕点P顺时针旋转90°后得到长方形A'B'C'D'(点B'、C'落在边AB上),请用a、b的代数式分别表示下列图形的面积.
(1)三角形PCC'的面积S1;
(2)四边形AA'CC'的面积S,并化简.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④若(﹣
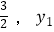 ),(
),( 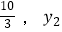 )是抛物线上两点,则y1<y2其中结论正确的是( )
)是抛物线上两点,则y1<y2其中结论正确的是( )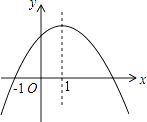
A.①②
B.②③
C.②④
D.①③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】分式中,在分子、分母都是整式的情况下,如果分子的次数低于分母的次数,称这样的分式为真分式.例如,分式是
 ,
, 是真分式.如果分子的次数不低于分母的次数,称这样的分式为假分式.例如,分式
是真分式.如果分子的次数不低于分母的次数,称这样的分式为假分式.例如,分式 ,
, 是假分式.一个假分式可以化为一个整式与一个真分式的和.例如,
是假分式.一个假分式可以化为一个整式与一个真分式的和.例如, =
= =1-
=1- .
.(1)将假分式
 化为一个整式与一个真分式的和;
化为一个整式与一个真分式的和;(2)如果分式
 的值为整数,求x的整数值.
的值为整数,求x的整数值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,E为BC上一点,AF平分∠DAE,求证:BE+DF=AE.
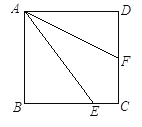
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校举办“大爱镇江”征文活动,小明为此次活动设计了一个以三座山为背景的图标(如图),现用红、黄两种颜色对图标中的A、B、C三块三角形区域分别涂色,一块区域只涂一种颜色.
(1)请用树状图列出所有涂色的可能结果;
(2)求这三块三角形区域中所涂颜色是“两块黄色、一块红色”的概率.
相关试题

