【题目】如图是二次函数y=ax2+bx+c的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④若(﹣ ![]() ),(
),( ![]() )是抛物线上两点,则y1<y2其中结论正确的是( )
)是抛物线上两点,则y1<y2其中结论正确的是( )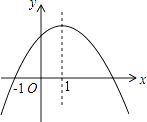
A.①②
B.②③
C.②④
D.①③④
参考答案:
【答案】C
【解析】解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=﹣ ![]() =1,
=1,
∴b=﹣2a>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①错误;
∵b=﹣2a,
∴2a+b=0,所以②正确;
∵抛物线与x轴的一个交点为(﹣1,0),抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点为(3,0),
∴当x=2时,y>0,
∴4a+2b+c>0,所以③错误;
∵点(﹣ ![]() )到对称轴的距离比点(
)到对称轴的距离比点( ![]() )对称轴的距离远,
)对称轴的距离远,
∴y1<y2,所以④正确.
所以答案是:C.
【考点精析】根据题目的已知条件,利用二次函数图象以及系数a、b、c的关系的相关知识可以得到问题的答案,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).
-
科目: 来源: 题型:
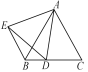
查看答案和解析>>【题目】如图,△ABC为等边三角形,点D为BC边上一动点(不与点B,C重合),∠DAE=60°,过点B作BE∥AC交AE于点E.
(1)求证:△ADE是等边三角形;
(2)当点D在何处时,AE⊥BE?指出点D的位置,并说明理由.
-
科目: 来源: 题型:
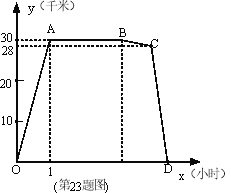
查看答案和解析>>【题目】(2011福建龙岩,23, 12分) 周六上午8:00小明从家出发,乘车1小时到郊外某基地参加社会实践活动,在基地活动2.2小时后,因家里有急事,他立即按原路以4千米/时的平均速度步行返回.同时爸爸开车从家出发沿同一路线接他,在离家28千米处与小明相遇。接到小明后保持车速不变,立即按原路返回.设小明离开家的时间为x小时,小名离家的路程y (干米) 与x (小时)之间的函致图象如图所示,
(1)小明去基地乘车的平均速度是________千米/小时,爸爸开车的平均速度应是________千米/小时;
(2)求线段CD所表示的函敛关系式;
(3)问小明能否在12:0 0前回到家?若能,请说明理由:若不能,请算出12:00时他离家的路程,
-
科目: 来源: 题型:
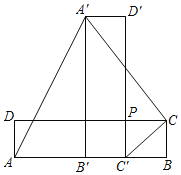
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=a,BC=b(a>2b),点P在边CD上,且PC=BC,长方形ABCD绕点P顺时针旋转90°后得到长方形A'B'C'D'(点B'、C'落在边AB上),请用a、b的代数式分别表示下列图形的面积.
(1)三角形PCC'的面积S1;
(2)四边形AA'CC'的面积S,并化简.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在正方形ABCD中,AE∥BD,BE=BD,BE交AD于F.求证:DE=DF.
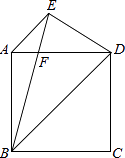
-
科目: 来源: 题型:
查看答案和解析>>【题目】分式中,在分子、分母都是整式的情况下,如果分子的次数低于分母的次数,称这样的分式为真分式.例如,分式是
 ,
, 是真分式.如果分子的次数不低于分母的次数,称这样的分式为假分式.例如,分式
是真分式.如果分子的次数不低于分母的次数,称这样的分式为假分式.例如,分式 ,
, 是假分式.一个假分式可以化为一个整式与一个真分式的和.例如,
是假分式.一个假分式可以化为一个整式与一个真分式的和.例如, =
= =1-
=1- .
.(1)将假分式
 化为一个整式与一个真分式的和;
化为一个整式与一个真分式的和;(2)如果分式
 的值为整数,求x的整数值.
的值为整数,求x的整数值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,E为BC上一点,AF平分∠DAE,求证:BE+DF=AE.
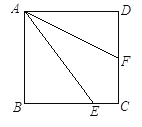
相关试题

