【题目】已知抛物线的解析式为y=﹣ ![]() x2+bx+5.
x2+bx+5.
(1)当自变量 x≥2时,函数值y 随 x的增大而减少,求b 的取值范围;
(2)如图,若抛物线的图象经过点A(2,5),与x 轴交于点C,抛物线的对称轴与x 轴交于B.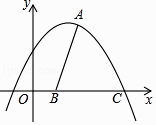
①求抛物线的解析式;
②在抛物线上是否存在点P,使得∠PAB=∠ABC?若存在,求出点P 的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:抛物线的对称轴为:x=10b,
由题意可知:x≥2时,函数值y 随 x的增大而减少,
∴10b≤2,
∴b≤ ![]()
(2)
解:①将A(2,5)代入抛物线的解析式中,
∴5=﹣ ![]() ×4+2b+5,
×4+2b+5,
∴b= ![]() ,
,
∴抛物线的解析式为:y=﹣ ![]() x2+
x2+ ![]() x+5,
x+5,
②由于∠PAB=∠ABC,
当P在对称轴的左侧时,
此时∠PAB=∠ABC,
∴PA∥BC,
∴P的纵坐标与A的纵坐标相同,
∴P(0,5),
当P在对称轴的右侧时,
连接AP并延长交x轴于E,
此时∠PAB=∠ABC
∴AE=BE,
过点A作AG⊥x轴于点G,过点P作PH⊥x轴于点H,过点E作EF⊥AB于点F,
∵B(1,0),A(2,5),
∴AG=5,BG=1,
∴由勾股定理可知:AB= ![]() ,
,
∵AE=BE,EF⊥AB,
∴BF= ![]() AB=
AB= ![]() ,
,
∵cos∠ABC= ![]() =
= ![]() ,
,
∴cos∠ABC= ![]() =
= ![]() ,
,
∴BE=13,
∴GE=BE﹣BG=12,
∴tan∠PEG= ![]() =
= ![]() ,
,
设P(x,﹣ ![]() x2+
x2+ ![]() x+5),
x+5),
∵E(14,0),
∴HE=14﹣x,PH=﹣ ![]() x2+
x2+ ![]() x+5,
x+5,
∴tan∠PEG= ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
解得:x=2(舍去)或x= ![]() ,
,
∴P( ![]() ,
, ![]() )
)
综上所述,P(0,5)或P( ![]() ,
, ![]() )
)

【解析】(1)由题意可知:对称轴只需要小于或等于2即可,从而可求出b的范围;(2)①将A代入抛物线解析式即可求出b的值.②由于∠PAB=∠ABC,且P在抛物线上,故需要对P的位置进行分类讨论即可.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
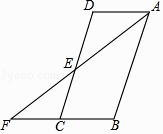
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°.求∠B的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某游乐场部分平面图如图所示,C、E、A在同一直线上,D、E、B在同一直线上,测得A处与E处的距离为80 米,C处与D处的距离为34米,∠C=90°,∠BAE=30°.(
 ≈1.4,
≈1.4,  ≈1.7)
≈1.7) 
(1)求旋转木马E处到出口B处的距离;
(2)求海洋球D处到出口B处的距离(结果保留整数). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点M在以O为圆心,AB为直径的半圆弧上运动(点M不与点A、B 及
 的中点F 重合),连接OM.过点M 作ME⊥AB于点E,以BE为边在半圆同侧作正方形BCDE,过点M作⊙O的切线交射线DC于点N,连接BM、BN.
的中点F 重合),连接OM.过点M 作ME⊥AB于点E,以BE为边在半圆同侧作正方形BCDE,过点M作⊙O的切线交射线DC于点N,连接BM、BN.
(1)探究:如图一,当动点M在 上运动时;
上运动时;
①判断△OEM∽△MDN是否成立?请说明理由;
②设 =k,k是否为定值?若是,求出该定值,若不是,请说明理由;
=k,k是否为定值?若是,求出该定值,若不是,请说明理由;
③设∠MBN=α,α是否为定值?若是,求出该定值,若不是,请说明理由;
(2)拓展:如图二,当动点M 在 上运动时;
上运动时;
分别判断(1)中的三个结论是否保持不变?如有变化,请直接写出正确的结论.(均不必说明理由) -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年5月份,某市测得一周大气的PM2.5的日均值(单位:微克/立方米)如下:31,35,31,33,30,33,31.对于这组数据下列说法正确的是( )
A.众数是30
B.中位数是31
C.平均数是33
D.方差是32 -
科目: 来源: 题型:
查看答案和解析>>【题目】形如半圆型的量角器直径为4cm,放在如图所示的平面直角坐标系中(量角器的中心与坐标原点O重合,零刻度线在x轴上),连接60°和120°刻度线的一个端点P、Q,线段PQ交y轴于点A,则点A的坐标为( )

A.(﹣1, )
)
B.(0, )
)
C.( ,0)
,0)
D.(1, )
)
相关试题

