【题目】如图,在楼房MN前有两棵树与楼房在同一直线上,且垂直于地面,为了测量树AB、CD的高度,小明爬到楼房顶部M处,光线恰好可以经过树CD的顶站C点到达树AB的底部B点,俯角为37°,此时小亮测得太阳光线恰好经过树CD的顶部C点到达楼房的底部N点,与地面的夹角为30°,树CD的影长DN为15米,请求出树AB和楼房MN的高度.
(![]() ,
,![]() ,
,![]() ,
,![]() ,结果精确到0.1m)
,结果精确到0.1m)

参考答案:
【答案】AB≈15.3米,楼高MN≈19.9米
【解析】分析:在Rt△CDN中,由于tan30°=![]() ,得到CD=tan30°DN=5
,得到CD=tan30°DN=5![]() ≈8.65,于是得到BD=
≈8.65,于是得到BD=![]() ,在Rt△ABN中,根据三角函数的定义即可得到结论;
,在Rt△ABN中,根据三角函数的定义即可得到结论;
详解:在Rt△CDN中,
∵tan30°=![]() ,
,
∴CD=tan30°DN=5![]() ≈8.65,,
≈8.65,,
∵∠CBD=37°,
∴BD=![]() ,
,
∴BN=DN+BD=11.53+15=26.53,
在Rt△ABN中,tan30°=![]() ,
,
∴AB=tan30°BN=![]() ×26.53≈15.3(米),
×26.53≈15.3(米),
在Rt△MNB中,MN=BNtan37°=0.75×26.53≈19.9(米)
∴树高AB是15.3米,楼房MN的高度是19.9米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分)如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD中,E是BC上一点,F是CD延长线上一点,
 ,连接AE,AF,EF,G为EF中点,连接AG,DG.
,连接AE,AF,EF,G为EF中点,连接AG,DG.
(1)如图1:若
 ,
, ,求DG;
,求DG;(2)如图2:延长GD至M,使
 ,过M作MN∥FD交AF的延长线于N,连接NG,若
,过M作MN∥FD交AF的延长线于N,连接NG,若 .求证:
.求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上两点之间的距离等于相应两数差的绝对值,即:点A、B表示的数分别为a、b,这两点之间的距离为AB=
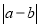 ,如:表示数1与5的两点之间的距离可表示为
,如:表示数1与5的两点之间的距离可表示为 ,表示数-2与3的两点之间的距离可表示为
,表示数-2与3的两点之间的距离可表示为 .
.(1)数轴上表示2和7的两点之间的距离是 ,数轴上表示3和-6的两点之间的距离是 ;
(2)数轴上表示x和-2的两点M和N之间的距离是 ,如果
 ,则x为 ;
,则x为 ;(3)当式子:
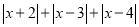 取最小值时,x的值为 ,最小值为 .
取最小值时,x的值为 ,最小值为 . (借助数轴,画出图形,写出过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】淘宝11.11购物节期间,小垣妈妈在网上某品牌服装店按标价八折拍到一件学生外套,用支付宝支付了120元.爱思考的小垣进行了下列研究:
(1)该学生外套在网上的标价是 元.
(2)妈妈告诉小垣她在网上买到的学生外套商家可以获得20%的利润.根据妈妈的说法,一件学生外套的进价是多少元?
(3)小垣搜索发现标价相同的同款学生外套在网上另一店铺打折优惠,并规定订单金额满200元,可以使用30元店铺优惠券.她告诉妈妈如果一次购买2件只需要支付225元,那么该网店同款学生外套打几折进行优惠?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校机器人兴趣小组在如图①所示的矩形场地上开展训练,机器人从点A出发,在矩形ABCD边上沿着A→B→C→D的方向匀速移动,到达点D时停止移动,已知AD=6个单位长度,机器人的速度为1个单位长度/s且其移动至拐角处调整方向所需时间忽略不计.设机器人所用时间为t(s)时,其所在位置用点P表示,P到对角线BD的距离(即垂线段PQ的长)为d个单位长度,其中d与t的函数图象如图②所示.
(1)图②中函数图象与纵轴的交点的纵坐标
 在图①中表示一条线段的长,请在图①中画出这条线段.
在图①中表示一条线段的长,请在图①中画出这条线段.(2)求图②中a的值;
(3)如图②,点M、N分别在线段EF、GH上,线段MN平行于横轴,M、N的横坐标分别为t1、t2.设机器人用了t1(s)到达点P1处,用了t2(s)到达点P2处(见图①).若CP1+CP2=7,求t1、t2的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,平行四边形ABCD在平面直角坐标系中,A、B(点A在点B的左侧)两点的横坐标是方程
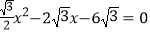 的两个根,点D在y轴上其中
的两个根,点D在y轴上其中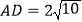 .
.
(1)求平行四边形ABCD的面积;
(2)若P是第一象限位于直线BD上方的一点,过P作
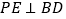 于E,过E作
于E,过E作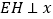 轴于H点,作PF∥y轴交直线BD于F,F为BD中点,其中△PEF的周长是
轴于H点,作PF∥y轴交直线BD于F,F为BD中点,其中△PEF的周长是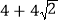 ;若M为线段AD上一动点,N为直线BD上一动点,连接HN,NM,求
;若M为线段AD上一动点,N为直线BD上一动点,连接HN,NM,求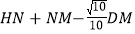 的最小值,此时y轴上有一个动点G,当
的最小值,此时y轴上有一个动点G,当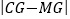 最大时,求G点坐标;
最大时,求G点坐标;(3)在(2)的情况下,将△AOD绕O点逆时针旋转60°后得到
 如图2,将线段
如图2,将线段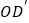 沿着x轴平移,记平移过程中的线段
沿着x轴平移,记平移过程中的线段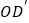 为
为 ,在平面直角坐标系中是否存在点S,使得以点
,在平面直角坐标系中是否存在点S,使得以点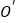 ,
,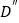 ,E,S为顶点的四边形为菱形,若存在,请求出点S的坐标,若不存在,请说明理由.
,E,S为顶点的四边形为菱形,若存在,请求出点S的坐标,若不存在,请说明理由.
相关试题

