Question

【题目】八年级某班同学为了了解2012年某居委会家庭月均用水情况，随机调查了该居委会部分家庭，并将调查数据进行如下调整：

月均用水量x（t）	频数（户）	频率
0＜x≤5	6	0.12
5＜x≤10	a	0.24
10＜x≤15	16	0.32
15＜x≤20	10	0.20
20＜x≤25	4	0.08
25＜x≤30	2	0.04

请解答以下问题：

（1）频数分布表中a=　 　，把频数分布直方图补充完整；

（2）求该居委会用水量不超过15t的家庭占被调查家庭总数的百分比；

（3）若该居委会有1000户家庭，根据调查数据估计，该小区月均用水量超过20t的家庭大约有多少户？

Answer 1

【答案】（1）12；（2）见解析；（3）120户.

【解析】

（1）首先求出样本数据进而得出a的值；

（2）利用用水量不超过15t的家庭数除以样本总数即可得出答案；

（3）直接利用样本估计总体得出该小区月均用水量超过20t的家庭数．

（1）由题意可得：样本数据为：=50，

则a=50×0.24=12，

如图所示：

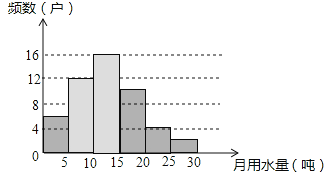
故答案为：12；

（2）由表格数据可得：该居委会用水量不超过15t的家庭占被调查家庭总数的百分比为：×100%=68%；

（3）由题意可得：×1000=120（户），

答：该小区月均用水量超过20t的家庭大约有120户．