【题目】观察、猜想、探究:
在△ABC中,![]() .
.
(1)如图①,当![]() ,AD为∠BAC的角平分线时,求证:
,AD为∠BAC的角平分线时,求证:![]() ;
;
(2)如图②,当![]() ,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的
,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的
数量关系?请写出你的猜想,并对你的猜想给予证明;
(3)如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?不需要证明,请直接写出你的猜想.



参考答案:
【答案】(1)见解析;(2 ) ![]() ,理由见解析;(3)
,理由见解析;(3)![]()
【解析】试题分析:(1)过D作DE⊥AB,交AB于点E,理由角平分线性质得到DE=DC,利用HL得到Rt△ACD≌Rt△AED,由全等三角形的对应边相等,对应角相等,得到AC=AE,∠ACB=∠AED,由∠ACB=2∠B,利用等量代换及外角性质得到一对角相等,利用等角对等边得到BE=DE=DC,由AB=BE+AE,等量代换即可得证;
(2)AB=CD+AC,理由为:在AB上截取AG=AC,如图2所示,由角平分线定义得到一对角相等,再由![]() ,利用SAS得到△ADG≌△ADC,接下来同(1)即可得证;
,利用SAS得到△ADG≌△ADC,接下来同(1)即可得证;
(3)AB=CDAC,理由为:在AF上截取AG=AC,如图3所示,同(2)即可得证.
试题解析:(1)过D作DE⊥AB,交AB于点E,如图1所示,
∵AD为∠BAC的平分线,DC⊥AC,DE⊥AB,
∴DE=DC,
在Rt△ACD和Rt△AED中,
AD=AD,DE=DC,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,∠ACB=∠AED,
∵∠ACB=2∠B,
∴∠AED=2∠B,
又∵∠AED=∠B+∠EDB,
∴∠B=∠EDB,
∴BE=DE=DC,
则AB=BE+AE=CD+AC;
(2)AB=CD+AC,理由为:
在AB上截取AG=AC,如图2所示,
∵AD为∠BAC的平分线,
∴∠GAD=∠CAD,
∵在△ADG和△ADC中,
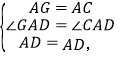
∴△ADG≌△ADC(SAS),
∴CD=DG,∠AGD=∠ACB,
∵∠ACB=2∠B,
∴∠AGD=2∠B,
又∵∠AGD=∠B+∠GDB,
∴∠B=∠GDB,
∴BE=DG=DC,
则AB=BG+AG=CD+AC;
(3)AB=CDAC,理由为:
在AF上截取AG=AC,如图3所示,
∵AD为∠FAC的平分线,
∴∠GAD=∠CAD,
∵在△ADG和△ACD中,
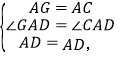
∴△ADG≌△ACD(SAS),
∴CD=GD,∠AGD=∠ACD,即∠ACB=∠FGD,
∵∠ACB=2∠B,
∴∠FGD=2∠B,
又∵∠FGD=∠B+∠GDB,
∴∠B=∠GDB,
∴BG=DG=DC,
则AB=BGAG=CDAC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣4,0),B(2,0),与y轴交于点C(0,2).

(1)求抛物线的解析式;
(2)若点D为该抛物线上的一个动点,且在直线AC上方,当以A,C,D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,
 ,AD平分∠CAB,交CB于点D,过点D作
,AD平分∠CAB,交CB于点D,过点D作 于点E.若
于点E.若 ,CD=5,.
,CD=5,.(1)求BD的长
(2)AE与BE相等吗?说明理由。
(3)求△ABC的面积

-
科目: 来源: 题型:
查看答案和解析>>【题目】在有些情况下,不需要计算出结果也能把绝对值符号去掉.例如:
|6+7|=6+7;|6-7|=7-6;|7-6|=7-6;|-6-7|=6+7;
根据上面的规律,把下列各式写成去掉绝对值符号的形式:
(1)|7-21|=_________;
(2)|
 |=____________;
|=____________;(3)|
 |=__________;
|=__________;(4)用合理的方法计算:|
 |+|
|+| |-
|- ×|-
×|- |+
|+ .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将两条宽度都为3的纸条重叠在一起,使∠ABC=60°,则四边形ABCD的面积为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)
(1)数轴上点B对应的数是______.
(2)经过几秒,点M、点N分别到原点O的距离相等?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC.
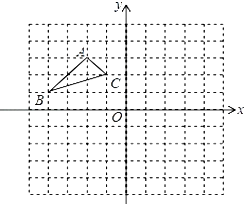
(1)作出△ABC关于x轴对称的△A1B1C1 , (只画出图形).
(2)作出△ABC关于原点O成中心对称的△A2B2C2 , (只画出图形),写出B2和C2的坐标.
相关试题

