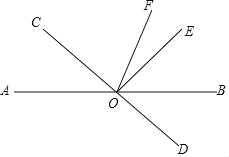
【题目】如图,直线AB,CD交于点O,OB平分∠DOE,OF是∠BOC的角平分线.
(1)说明:∠AOC=∠BOE;
(2)若∠AOC=46°,求∠EOF的度数;
(3)若∠EOF=30°,求∠AOC的度数.
参考答案:
【答案】(1)证明见解析;(2)∠EOF=21°;(3)∠AOC=40°.
【解析】
(1)根据角平分线的定义得到∠BOE=∠BOD,根据角的和差即可得到结论;
(2)根据邻补角的定义得到∠BOC=180°﹣∠AOC=134°,∠BOE=46°,根据角平分线的定义得到∠BOF=![]() ∠BOC=67°,于是得到结论;
∠BOC=67°,于是得到结论;
(3)设∠AOC=α,则∠BOE=α,得到∠BOF=α+30°,由OF是∠BOC的角平分线,得到∠BOC=2∠BOF=2α+60°,于是得到结论.
解:(1)∵OB平分∠DOE,
∴∠BOE=∠BOD,
∵∠AOC=∠BOD,
∴∠AOC=∠BOE;
(2)∵∠AOC=46°,
∴∠BOC=180°﹣∠AOC=134°,∠BOE=46°,
∵OF是∠BOC的角平分线,
∴∠BOF=![]() ∠BOC=67°,
∠BOC=67°,
∴∠EOF=∠BOF﹣∠BOE=21°;
(3)设∠AOC=α,则∠BOE=α,
∵∠EOF=30°,
∴∠BOF=α+30°,
∵OF是∠BOC的角平分线,
∴∠BOC=2∠BOF=2α+60°,
∴α=180°﹣(2α+60°),
∴α=40°,
∴∠AOC=40°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ANCD中,AD=5,CD=3,在直线BC上取一点E,使△ADE是以DE为底的等腰三角形,过点D作直线AE的垂线,垂足为点F,则EF= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)-15-[-1-(4-22×5)]
(2)-12019-(1-
 )÷|3-(-3)2|
)÷|3-(-3)2| -
科目: 来源: 题型:
查看答案和解析>>【题目】若将一幅三角板按如图所示的方式放置,则下列结论中不正确的是( )

A. ∠1=∠3 B. 如果∠2=30°,则有AC∥DE
C. 如果∠2=30°,则有BC∥AD D. 如果∠2=30°,必有∠4=∠C
-
科目: 来源: 题型:
查看答案和解析>>【题目】Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.

(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2= °;
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间有何关系?说明理由.
(3)若点P在Rt△ABC斜边BA的延长线上运动(CE<CD),则∠α、∠1、∠2之间有何关系?猜想并说明理由.
-
科目: 来源: 题型:
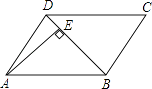
查看答案和解析>>【题目】如图,平行四边形ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAE等于( )
A.20°
B.25°
C.30°
D.35° -
科目: 来源: 题型:
查看答案和解析>>【题目】为了推动“龙江经济带”建设,我省某蔬菜企业决定通过加大种植面积、增加种植种类,促进经济发展,2017年春,预计种植西红柿、马铃薯、青椒共100公顷(三种蔬菜的种植面积均为整数),青椒的种植面积是西红柿种植面积的2倍,经预算,种植西红柿的利润可达1万元/公顷,青椒1.5万元/公顷,马铃薯2万元/公顷,设种植西红柿x公顷,总利润为y万元.
(1)求总利润y(万元)与种植西红柿的面积x(公顷)之间的关系式.
(2)若预计总利润不低于180万元,西红柿的种植面积不低于8公顷,有多少种种植方案?
(3)在(2)的前提下,该企业决定投资不超过获得最大利润的
 在冬季同时建造A、B两种类型的温室大棚,开辟新的经济增长点,经测算,投资A种类型的大棚5万元/个,B种类型的大棚8万元/个,请直接写出有哪几种建造方案?
在冬季同时建造A、B两种类型的温室大棚,开辟新的经济增长点,经测算,投资A种类型的大棚5万元/个,B种类型的大棚8万元/个,请直接写出有哪几种建造方案?
相关试题

