【题目】十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(![]() )、面数(
)、面数(![]() )、棱数(
)、棱数(![]() )之间存在的一个有趣的关系式,被称为欧拉公式,请你观察下列几种简单多面体模型,解答下列问题:
)之间存在的一个有趣的关系式,被称为欧拉公式,请你观察下列几种简单多面体模型,解答下列问题:
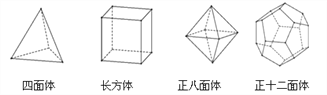
(1)根据上面多面体模型,完成表格中的空格;
多面体 | 顶点数( | 面数( | 棱数( |
四面体 |
|
| |
长方体 |
|
|
|
正八面体 |
|
| |
正十二面体 |
|
|
|
(1)你发现顶点数(![]() )、面数(
)、面数(![]() )、棱数(
)、棱数(![]() )之间存在的关系式是_______.
)之间存在的关系式是_______.
(2)正十二面体有![]() 个顶点,那它有______条棱;
个顶点,那它有______条棱;
(3)一个多面体的面数比顶点数大![]() ,且有
,且有![]() 条棱,则这多面体的顶点数是______;
条棱,则这多面体的顶点数是______;
(4)某个玻璃饰品的外形是简单多面体,它的外表是由三角形和八边形两种多边形拼接而成,且有![]() 个顶点,每个顶点处都有
个顶点,每个顶点处都有![]() 条棱,设该多面体表面三角形的个数为
条棱,设该多面体表面三角形的个数为![]() 个,八边形的个数为
个,八边形的个数为![]() 个,求
个,求![]() 的值.
的值.
参考答案:
【答案】填表见解析;(1)![]() ;(2)30;(3)12;(4)26.
;(2)30;(3)12;(4)26.
【解析】(1)
多面体 | 顶点数( | 面数( | 棱数( |
四面体 |
|
|
|
长方体 |
|
|
|
正八面体 |
|
|
|
正十二面体 |
|
|
|
![]()
(2)![]() 条棱
条棱
解析:![]() ,
,![]()
(3)解析:顶点数为![]() ,,面为
,,面为![]()
![]()
解得![]()
(4)解:∵有![]() 个顶点,
个顶点,![]() 个顶点确定一条棱,每个顶点
个顶点确定一条棱,每个顶点![]() 个棱
个棱
∴![]() (条)
(条)
![]()
解得![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明“在一个三角形中,至少有一个内角小于或等于60°”时应假设( )
A. 三角形中有一个内角小于或等于60° B. 三角形中有两个内角小于或等于60°
C. 三角形中有三个内角小于或等于60° D. 三角形中没有一个内角小于或等于60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,AC=16cm,CB=12cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由.
(3)若C在线段AB的延长线上,且满足AC﹣BC=b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,不要说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D、E、F分别在BC、AB、AC上,且DE∥AC,DF∥AB.
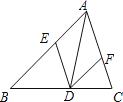
(1)如果∠BAC=90°,那么四边形AEDF是 形;
(2)如果AD是△ABC的角平分线,那么四边形AEDF是 形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC=10,BD=24,

(1)点E、F分别是边AB、BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是 ;
(2)点E、F、P分别在线段AB、BC、AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解a2b﹣b的正确结果是( )
A. b(a+1)(a ﹣1) B. a(b+1)(b﹣1) C. b(a2﹣1) D. b(a﹣1)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】
A. 9 B. -9 C. 15 D. -15
相关试题

