【题目】如图,在菱形ABCD中,对角线AC=10,BD=24,

(1)点E、F分别是边AB、BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是 ;
(2)点E、F、P分别在线段AB、BC、AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是 .
参考答案:
【答案】(1)13;(2)![]() .
.
【解析】
试题解析:(1)如图1中,取CD中点M,连接EM与AC交于点P,PE+PF的最小值=PE+PM=EM,由此即可解决问题.
(2)如图2,作点F关于AC的对称点M,连接EM与AC交于点P,当EM⊥CD时,PE+PF=PE+PM=EM,此时PE+PF最短,由此即可解决问题.
解:(1)如图1,

取CD中点M,连接EM与AC交于点P,
∵四边形ABCD是菱形,AC=10,DB=24,
∴AC⊥BD,AD=AB=![]() =13,
=13,
∵DM=MC,CF=FB,CD、CB关于AC对称,
∴M、F关于AC对称,
∴PE+PF=PE+PM=EM最小,
∵AE=EB.DM=MC,
∴AE=DM.AE∥DM,
∴四边形ADME是平行四边形,∴ME=AD=13.
(2)如图2,

作点F关于AC的对称点M,连接EM与AC交于点P,
当EM⊥CD时,PE+PF=PE+PM=EM,此时PE+PF最短(垂线段最短),
∵S菱形ABCD=![]() ACBD=
ACBD=![]() ABEM,
ABEM,
∴![]() ×10×24=
×10×24=![]() ×13×EM,
×13×EM,
∴EM=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,AC=16cm,CB=12cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由.
(3)若C在线段AB的延长线上,且满足AC﹣BC=b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,不要说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D、E、F分别在BC、AB、AC上,且DE∥AC,DF∥AB.
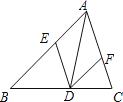
(1)如果∠BAC=90°,那么四边形AEDF是 形;
(2)如果AD是△ABC的角平分线,那么四边形AEDF是 形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(
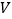 )、面数(
)、面数(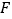 )、棱数(
)、棱数(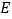 )之间存在的一个有趣的关系式,被称为欧拉公式,请你观察下列几种简单多面体模型,解答下列问题:
)之间存在的一个有趣的关系式,被称为欧拉公式,请你观察下列几种简单多面体模型,解答下列问题: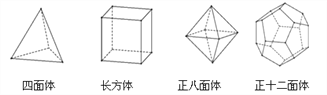
(1)根据上面多面体模型,完成表格中的空格;
多面体
顶点数(
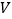 )
)面数(
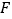 )
)棱数(
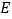 )
)四面体


长方体

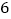
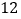
正八面体

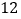
正十二面体
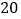
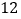
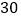
(1)你发现顶点数(
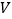 )、面数(
)、面数(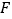 )、棱数(
)、棱数(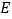 )之间存在的关系式是_______.
)之间存在的关系式是_______.(2)正十二面体有
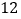 个顶点,那它有______条棱;
个顶点,那它有______条棱;(3)一个多面体的面数比顶点数大
 ,且有
,且有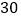 条棱,则这多面体的顶点数是______;
条棱,则这多面体的顶点数是______;(4)某个玻璃饰品的外形是简单多面体,它的外表是由三角形和八边形两种多边形拼接而成,且有
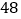 个顶点,每个顶点处都有
个顶点,每个顶点处都有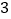 条棱,设该多面体表面三角形的个数为
条棱,设该多面体表面三角形的个数为 个,八边形的个数为
个,八边形的个数为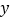 个,求
个,求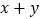 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解a2b﹣b的正确结果是( )
A. b(a+1)(a ﹣1) B. a(b+1)(b﹣1) C. b(a2﹣1) D. b(a﹣1)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】
A. 9 B. -9 C. 15 D. -15
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面的多项式在实数范围内能因式分解的是( )
A.x2+y2 B.x2﹣y C.x2+x+1 D.x2﹣2x+1
相关试题

