【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

参考答案:
【答案】(1)![]() ;(2)45°;(3)
;(2)45°;(3)![]() .
.
【解析】试题分析: ![]() 把点
把点![]() 的坐标代入即可求得抛物线的解析式.
的坐标代入即可求得抛物线的解析式.
![]() 作BH⊥AC于点H,求出
作BH⊥AC于点H,求出![]() 的长度,即可求出∠ACB的度数.
的长度,即可求出∠ACB的度数.
![]() 延长CD交x轴于点G,△DCE∽△AOC,只可能∠CAO=∠DCE.求出直线
延长CD交x轴于点G,△DCE∽△AOC,只可能∠CAO=∠DCE.求出直线![]() 的方程,和抛物线的方程联立即可求得点
的方程,和抛物线的方程联立即可求得点![]() 的坐标.
的坐标.
试题解析:(1)由题意,得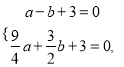
解得![]() .
.
∴这条抛物线的表达式为![]() .
.
(2)作BH⊥AC于点H,
∵A点坐标是(-1,0),C点坐标是(0,3),B点坐标是(![]() ,0),
,0),
∴AC=![]() ,AB=
,AB=![]() ,OC=3,BC=
,OC=3,BC=![]() .
.
∵![]() ,即∠BAD=
,即∠BAD= ![]() ,
,
∴![]() .
.
Rt△ BCH中, ![]() ,BC=
,BC=![]() ,∠BHC=90,
,∠BHC=90,
∴![]() .
.
又∵∠ACB是锐角,∴![]() .
.
(3)延长CD交x轴于点G,
∵Rt△ AOC中,AO=1,AC=![]() ,
,
∴![]() .
.
∵△DCE∽△AOC,∴只可能∠CAO=∠DCE.
∴AG = CG.
∴ .
.
∴AG=5.∴G点坐标是(4,0).
∵点C坐标是(0,3),∴![]() .
.
∴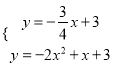 解得
解得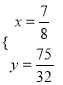 ,
, ![]() (舍).
(舍).
∴点D坐标是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F,∠1=∠2.
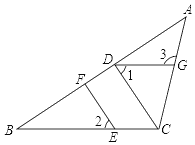
(1)试说明DG∥BC的理由;
(2)如果∠B=34°,且∠ACD=47°,求∠3的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】歼-20(英文:Chengdu J-20,绰号:威龙,北约命名:Fire Fang)是我国自主研发的一款单座、双发动机并具备高隐身性、高态势感知、高机动性等能力的第五代战斗机。


歼-20在机腹部位有一个主弹仓,机身两侧的起落架前方各有一个侧弹仓。歼-20的侧弹舱门为一片式结构,这个弹舱舱门向上开启,弹舱内滑轨的前端向外探出,使导弹头部伸出舱外,再直接点火发射。
如图是歼-20侧弹舱内部结构图,它的舱体横截面是等腰梯形ABCD,AD//BC,AB = CD,BE⊥AD,CF⊥AD,侧弹舱宽AE = 2.3米,舱底宽BC = 3.94米,舱顶与侧弹舱门的夹角∠A = 53.
求(1)侧弹舱门AB的长;
(2)舱顶AD与对角线BD的夹角的正切值.(结果精确到0.01,参考数据:
 ,
,  ,
,  ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
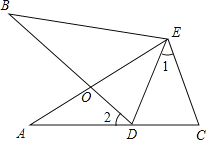
(1)求证:∠BDE=∠C;
(2)求证:△AEC≌△BED;
(3)若∠2=40°,则∠BDE=______°.
-
科目: 来源: 题型:
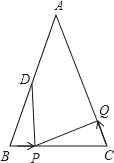
查看答案和解析>>【题目】如图,已知△ABC中,AB=6cm,∠B=∠C,BC=4cm,点D为AB的中点.若点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知M的横坐标是
 的平方根,纵坐标是2,且点M到y轴的距离是到x轴的距离的3倍。
的平方根,纵坐标是2,且点M到y轴的距离是到x轴的距离的3倍。(1)求a的值;
(2)求点M的坐标。
相关试题

