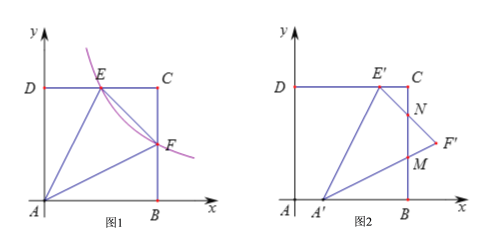
【题目】如图1,正方形ABCD的边长为4,以AB所在的直线为x轴,以AD所在的直线为y轴建立平面直角坐标系![]() 反比例函数
反比例函数![]() 的图象与CD交于E点,与CB交于F点.
的图象与CD交于E点,与CB交于F点.
(1)求证:![]() ;
;
(2)若![]() 的面积为6,求反比例函数的解析式;
的面积为6,求反比例函数的解析式;
(3)在(2)的条件下,将![]() 沿x轴的正方向平移1个单位后得到
沿x轴的正方向平移1个单位后得到![]() ,如图2,线段
,如图2,线段![]() 与
与![]() 相交于点M,线段
相交于点M,线段![]() 与BC相交于点N.求
与BC相交于点N.求![]() 与正方形ABCD的重叠部分面积.
与正方形ABCD的重叠部分面积.
参考答案:
【答案】(1)证明见解析;(2)反比例函数解析式为![]() ;(3)
;(3)![]() =
=![]() .
.
【解析】(1)根据反比例函数图象上点的坐标特点可得出DE=BF,故可得出结论;
(2)设DE=BF=a,则CE=4-a,CF=4-a,再由S△AEF=S正方形ABCD-S△ADE-S△ABF-S△ECF即可得出a的值,进而可得出反比例函数的解析式;
(3)根据题意求得N点的坐标,再求出直线![]() 的解析式,进而得到M点的坐标,然后由阴影部分分解图形的面积公式求解即可.
的解析式,进而得到M点的坐标,然后由阴影部分分解图形的面积公式求解即可.
(1)由题意知:![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
在![]() 和
和![]() 中
中
∴![]() ≌
≌![]() (SAS)
(SAS)
∴![]() .
.
(2)由(1)知:![]()
∴![]()
∵![]()
∴![]()
∴![]()
又∵![]()
∴![]()
∴反比例函数解析式为:![]() .
.
(3)由题意得:![]() ,
,![]() ,
,![]()
由(1)知:![]()
∴![]()
设直线![]() 的解析式为:
的解析式为:![]()
把点![]() ,
,![]() 代入得:
代入得:
![]()
解之得:
∴![]()
∴![]()
∴![]()
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图像与反比例函数
的图像与反比例函数 的图像交于点
的图像交于点 和点
和点 .
.(1)求一次函数和反比例函数的解析式;
(2)直接写出不等式
 的解集;
的解集;(3)若点A关于y轴的对称点为C,问是否在x轴下方存在一点D,使以点A、B、C、D为顶点的四边形是平行四边形.若存在,直接写出点D的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图1。在图2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换。若骰子的初始位置为图1所示的状态,那么按上述规则连续完成14次变换后,骰子朝上一面的点数是_____________________。

-
科目: 来源: 题型:
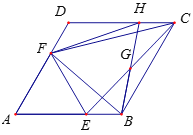
查看答案和解析>>【题目】如图,在菱形ABCD中,
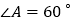 .点E、F分别是边AB、AD上的点,且满足
.点E、F分别是边AB、AD上的点,且满足 ,连结EF.
,连结EF.(1)求证:
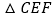 为等腰三角形;
为等腰三角形;(2)若
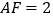 ,求
,求 的面积;
的面积;(3)若G是CE的中点,连结BG并延长交DC于点H,连结FH,求证:
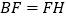 .
. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,点A、O、B依次在直线MN上,现将射线OA绕点O沿顺时针方向以每秒2°的速度旋转,同时射线OB绕点O沿逆时针方向以每秒4°的速度旋转,如图2,设旋转时间为t(0秒≤t≤90秒).
(1)用含t的代数式表示∠MOA的度数.
(2)在运动过程中,当∠AOB第二次达到60°时,求t的值.
(3)在旋转过程中是否存在这样的t,使得射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角(指大于0°而不超过180°的角)的平分线?如果存在,请直接写出t的值;如果不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,∠ABC的平分线交AD于点E,∠BED的平分线交DC于点F,若AB=6,点F恰为DC的中点,则BC=(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,CP平分∠ACB,其中正确的是( )
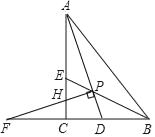
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
相关试题

