【题目】如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,CP平分∠ACB,其中正确的是( )
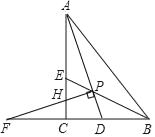
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
参考答案:
【答案】D
【解析】根据三角形内角和定理以及角平分线定义判断①;根据全等三角形的判定和性质判断②③;根据角平分线的判定与性质判断④.
在△ABC中,∵∠ACB=90°,
∴∠BAC+∠ABC=90°,
又∵AD、BE分别平分∠BAC、∠ABC,
∴∠BAD+∠ABE=![]() (∠BAC+∠ABC)=45°,
(∠BAC+∠ABC)=45°,
∴∠APB=135°,故①正确.
∴∠BPD=45°,
又∵PF⊥AD,
∴∠FPB=90°+45°=135°,
∴∠APB=∠FPB,
又∵∠ABP=∠FBP,BP=BP,
∴△ABP≌△FBP,
∴∠BAP=∠BFP,AB=FB,PA=PF,故②正确.
在△APH和△FPD中,
∵∠APH=∠FPD=90°,∠PAH=∠BAP=∠BFP,PA=PF,
∴△APH≌△FPD,
∴PH=PD,故③正确.
∵△ABC的角平分线AD、BE相交于点P,
∴点P到AB、AC的距离相等,点P到AB、BC的距离相等,
∴点P到BC、AC的距离相等,
∴点P在∠ACB的平分线上,
∴CP平分∠ACB,故④正确.
故选:D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形ABCD的边长为4,以AB所在的直线为x轴,以AD所在的直线为y轴建立平面直角坐标系
 反比例函数
反比例函数 的图象与CD交于E点,与CB交于F点.
的图象与CD交于E点,与CB交于F点.(1)求证:
 ;
;(2)若
 的面积为6,求反比例函数的解析式;
的面积为6,求反比例函数的解析式;(3)在(2)的条件下,将
 沿x轴的正方向平移1个单位后得到
沿x轴的正方向平移1个单位后得到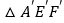 ,如图2,线段
,如图2,线段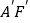 与
与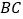 相交于点M,线段
相交于点M,线段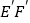 与BC相交于点N.求
与BC相交于点N.求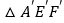 与正方形ABCD的重叠部分面积.
与正方形ABCD的重叠部分面积.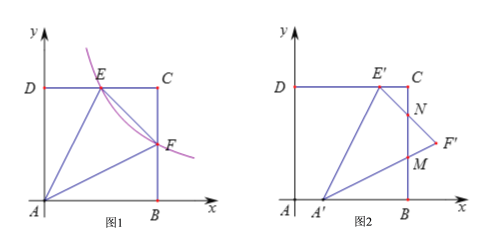
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,点A、O、B依次在直线MN上,现将射线OA绕点O沿顺时针方向以每秒2°的速度旋转,同时射线OB绕点O沿逆时针方向以每秒4°的速度旋转,如图2,设旋转时间为t(0秒≤t≤90秒).
(1)用含t的代数式表示∠MOA的度数.
(2)在运动过程中,当∠AOB第二次达到60°时,求t的值.
(3)在旋转过程中是否存在这样的t,使得射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角(指大于0°而不超过180°的角)的平分线?如果存在,请直接写出t的值;如果不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,∠ABC的平分线交AD于点E,∠BED的平分线交DC于点F,若AB=6,点F恰为DC的中点,则BC=(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】新年晚会,是我们最欢乐的时候.会场上,悬挂着五彩缤纷的小装饰,其中有各种各样的立体图形,如图所示.
(1)数一下每一个多面体具有的顶点数
 、棱数
、棱数 和面数
和面数 .并且把结果记入表中.
.并且把结果记入表中.多面体
顶点数

面数

棱数

正四面体
4
4
6
正方体
正八面体
正十二面体
正二十面体
12
20
30
(2)观察表中数据,猜想多面体的顶点数
 、棱数
、棱数 和面数
和面数 之间的关系.
之间的关系.(3)伟大的数学家欧拉(Euler,1707-1783)证明了这一令人惊叹的关系式,即欧拉公式.若已知一个多面体的顶点数
 =196,棱数
=196,棱数 =294.请你用欧拉公式求这个多面体的面数.
=294.请你用欧拉公式求这个多面体的面数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(1,2),B(3,1),C(﹣2,﹣1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1.
(2)直接写出点A1,B1,C1的坐标.
A1 , B1 , C1 ;
(3)请你求出△A1B1C1的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】以直线AB上一点O为端点作射线OC,将一块直角三角板的直角顶点放在O处(注:∠DOE=90°).
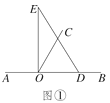

(1)如图①,若直角三角板DOE的一边OD放在射线OB上,且∠BOC=60°,求∠COE的度数;
(2)如图②,将三板DOE绕O逆时针转动到某个位置时,若恰好满足5∠COD=∠AOE,且∠BOC=60°,求∠BOD的度数;
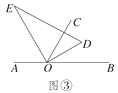
(3)如图③,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线.
相关试题

