【题目】平面直角坐标系中,A(m,0)、B(m+1,0)、E(2,0),其中-1≤m≤2,分别以AB、OE为边向上作正方形ABCD、OEFG.
(1)请直接写出线段AB的长;
(2)正方形ABCD沿x轴正半轴运动过程中与正方形OEFG重叠部分面积为S,求S与m的关系式.
参考答案:
【答案】(1)1;(2)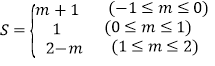
【解析】
(1)线段AB的长度由点B的横坐标减去A点的横坐标即可得;
(2)分三种情况讨论:当-1≤m≤0时、当1≤m≤2时和当1≤m≤2时进行分析即可;
(1)∵A(m,0)、B(m+1,0),
∴AB=m+1-m=1;
(2)∵A(m,0)、B(m+1,0)
∴AB=1,
∴正方形ABCD的边长为1
如图1,当-1≤m≤0时
S=OB![]() BC=m+1
BC=m+1
如图2,当0≤m≤1时
S=AB![]() AD=1
AD=1
如图3,当1≤m≤2时
AE=OE-OA=2-m
S=AE![]() AD=2-m.
AD=2-m.
综上所述,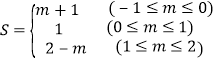
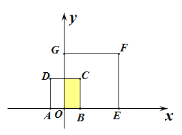
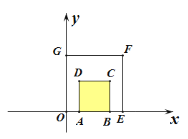
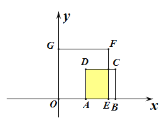
图1 图2 图3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市文化宫学习十九大有关优先发展教育的精神,举办了为某贫困山区小学捐赠书包活动.首次用2000元在商店购进一批学生书包,活动进行后发现书包数量不够,又购进第二批同样的书包,所购数量是第一批数量的3倍,但单价贵了4元,结果第二批用了6300元.
(1)求文化官第一批购进书包的单价是多少?
(2)商店两批书包每个的进价分别是68元和70元,这两批书包全部售给文化宫后,商店共盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句:①有一边对应相等的两个直角三角形全等;②一般三角形具有的性质,直角三角形都具有;③有两边相等的两直角三角形全等;④两直角三角形的斜边为5cm,一条直角边都为3cm,则这两个直角三角形必全等.其中正确的有________个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小明遇到这样一个问题:
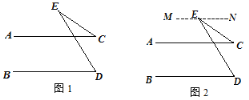
(1)如图1,AC∥BD,点E为直线AC上方一点,连接CE、DE,猜想∠C、∠D、∠E的数量关系,并证明.小明发现,可以过点E作MN∥AC来解决问题,如图2,请你完成解答:
(2)用学过的知识或参考小明的方法,解决下面的问题:
如图3,AB∥CD,P是平面内一点,连接AP、CP,使AP∥BD,∠APC=100°,BM、CM分别平分∠ABD,∠DCP交于点M,求∠M的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.
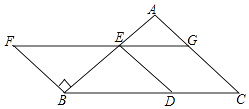
(1)求证:四边形BDEF为平行四边形;
(2)当∠C=45°,BD=2时,求D,F两点间的距离. -
科目: 来源: 题型:
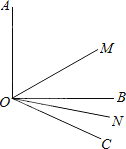
查看答案和解析>>【题目】如图所示,已知∠AOB=90°,∠BOC=20°,OM平分∠AOC,ON平分∠BOC;
(1)求∠MON;
(2)∠AOB=α,∠BOC=β,求∠MON的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.

现有38张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,则能做多少个盒子?
相关试题

