【题目】如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.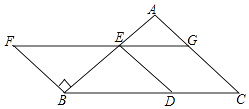
(1)求证:四边形BDEF为平行四边形;
(2)当∠C=45°,BD=2时,求D,F两点间的距离.
参考答案:
【答案】
(1)证明:∵△ABC是等腰三角形,
∴∠ABC=∠C,
∵EG∥BC,DE∥AC,
∴∠AEG=∠ABC=∠C,四边形CDEG是平行四边形,
∴∠DEG=∠C,
∵BE=BF,
∴∠BFE=∠BEF=∠AEG=∠ABC,
∴∠F=∠DEG,
∴BF∥DE,
∴四边形BDEF为平行四边形;
(2)解:∵∠C=45°,
∴∠ABC=∠BFE=∠BEF=45°,
∴△BDE、△BEF是等腰直角三角形,
∴BF=BE= ![]() BD=
BD= ![]() ,
,
作FM⊥BD于M,连接DF,如图所示: 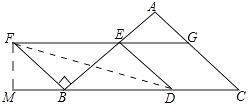
则△BFM是等腰直角三角形,
∴FM=BM= ![]() BF=1,
BF=1,
∴DM=3,
在Rt△DFM中,由勾股定理得:DF= ![]() =
= ![]() ,
,
即D,F两点间的距离为 ![]() .
.
【解析】(1)要证四边形BDEF为平行四边形由已知EG∥BC,须证BF∥DE,可利用等腰三角形的性质先证四边形CDEG是平行四边形,得出∠DEG=∠C,再通过转化证出BF∥DE;(2)要求DF距离须把DF放在直角三角形中,因此需过F作BD的垂线构造直角三角形,可证出△BDE、△BEF是等腰直角三角形,由BD求出DE,进而求出BF、MF,由勾股定理求出DF.
【考点精析】本题主要考查了等腰三角形的性质和平行四边形的判定与性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句:①有一边对应相等的两个直角三角形全等;②一般三角形具有的性质,直角三角形都具有;③有两边相等的两直角三角形全等;④两直角三角形的斜边为5cm,一条直角边都为3cm,则这两个直角三角形必全等.其中正确的有________个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小明遇到这样一个问题:
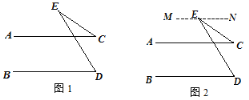
(1)如图1,AC∥BD,点E为直线AC上方一点,连接CE、DE,猜想∠C、∠D、∠E的数量关系,并证明.小明发现,可以过点E作MN∥AC来解决问题,如图2,请你完成解答:
(2)用学过的知识或参考小明的方法,解决下面的问题:
如图3,AB∥CD,P是平面内一点,连接AP、CP,使AP∥BD,∠APC=100°,BM、CM分别平分∠ABD,∠DCP交于点M,求∠M的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,A(m,0)、B(m+1,0)、E(2,0),其中-1≤m≤2,分别以AB、OE为边向上作正方形ABCD、OEFG.
(1)请直接写出线段AB的长;
(2)正方形ABCD沿x轴正半轴运动过程中与正方形OEFG重叠部分面积为S,求S与m的关系式.
-
科目: 来源: 题型:
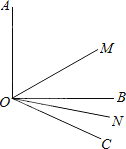
查看答案和解析>>【题目】如图所示,已知∠AOB=90°,∠BOC=20°,OM平分∠AOC,ON平分∠BOC;
(1)求∠MON;
(2)∠AOB=α,∠BOC=β,求∠MON的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.

现有38张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,则能做多少个盒子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
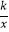 的图象与一次函数y=x+b的图象交于A,B两点,点A和点B的横坐标分别为1和﹣2,这两点的纵坐标之和为1.
的图象与一次函数y=x+b的图象交于A,B两点,点A和点B的横坐标分别为1和﹣2,这两点的纵坐标之和为1.
(1)求反比例函数的表达式与一次函数的表达式;
(2)当点C的坐标为(0,﹣1)时,求△ABC的面积.
相关试题

