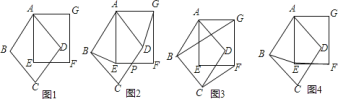
【题目】我们给定两个全等的正方形![]() 、
、![]() ,它们共顶点
,它们共顶点![]() (如图
(如图![]() ),可以绕顶点
),可以绕顶点![]() 旋转,
旋转,![]() ,
,![]() 相交于点
相交于点![]() ,以下各问题都以此为前提.
,以下各问题都以此为前提.
问题要求:
![]() 连接
连接![]() 、
、![]() (如图
(如图![]() ),求证:
),求证:![]() ,
,![]() ;
;
![]() 连接
连接![]() 、
、![]() (如图
(如图![]() ),有三个结论:
),有三个结论:
①![]() ;
;
②![]() ;
;
③![]() 与
与![]() 位似.
位似.
请你从①,②,③三个结论中选择一个进行证明:
(说明:选①做对的得![]() 分,选②做对的得
分,选②做对的得![]() 分,选③做对的得
分,选③做对的得![]() 分)
分)
![]() 连接
连接![]() 、
、![]() (如图
(如图![]() ),求
),求![]() 的值.
的值.
参考答案:
【答案】(1)证明见解析;(2)①证明见解析;②证明见解析;③![]() .
.
【解析】
(1)根据正方形的性质,即可得AB=AD,∠BAE=90°﹣∠EAD=∠DAG,AE=AG,由边角边判定方法即可证得△ABE≌△ADG,即BE=DG;∵△ABE≌△ADG,AB⊥AD,AE⊥AG,所以△ADG可以看成由△ABE绕顶点A旋转90°,即BE⊥DG;
(2)根据等边对等角即可证得BG∥CF;根据平行线的性质可的对应角相等,即可证得②△ABG∽△PCF;续②连接AP交GF的延长线于Q1,交BC的延长线于Q2,由位似的性质即可求得;
(3)连接AC,AF,CF.可证得△ABE∽△ACF,根据相似三角形的性质即可求得.
(1)∵AB=AD,∠BAE=90°﹣∠EAD=∠DAG,AE=AG,∴△ABE≌△ADG,即BE=DG.
分别延长GD,BE交于点M交EF于点N.
∵∠MEN+∠ENM=∠MEN+∠AGD=∠BEA+∠NEM=90°,∴BE⊥GD.
(∵△ABE≌△ADG,AB⊥AD,AE⊥AG,∴△ADG可以看成由△ABE绕顶点A旋转90°,即BE⊥DG.)
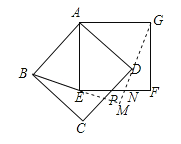
(2)①∵AB=AG,∴∠ABG=∠AGB,∠CBG=∠FGB,∴∠GBC=∠BGF.
又∵BC=GF,∴∠BCF=∠GFC.
又∵∠CBG+∠FGB+∠BCF+∠GFC=360°,∴∠CBG+∠BCF=180°,即BG∥CF;
②续①又∵AB∥PC,AG∥PF,∴∠ABG=∠PCF,∠AGB=∠PFC即△ABG∽△PCF;
③续②连接AP交GF的延长线于Q1,交BC的延长线于Q2,则![]() =
=![]() =
=![]() ,而AB=AG,PC=PF,∴
,而AB=AG,PC=PF,∴![]() =
=![]() ,亦有
,亦有![]() =
=![]() ,Q1P=Q2P,∴Q1,Q2重合,即BC,AP,GF相交于点Q,△ABG与△PCF位似.
,Q1P=Q2P,∴Q1,Q2重合,即BC,AP,GF相交于点Q,△ABG与△PCF位似.
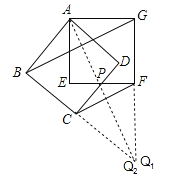
(3)连接AC,AF,CF.
∵ABCD和AEFG都是正方形,∴CA=![]() AB,AF=
AB,AF=![]() AE,∠BAC=∠EAF=45°,∴AC:AF=
AE,∠BAC=∠EAF=45°,∴AC:AF=![]() AB:
AB:![]() AE=AB:AE,∠BAE=∠CAF,∴△ABE∽△ACF,
AE=AB:AE,∠BAE=∠CAF,∴△ABE∽△ACF,![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(问题情境)如图
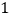 ,
,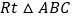 中,
中,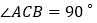 ,
,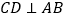 ,我们可以利用
,我们可以利用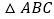 与
与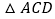 相似证明
相似证明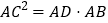 ,这个结论我们称之为射影定理,试证明这个定理;
,这个结论我们称之为射影定理,试证明这个定理;(结论运用)如图
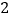 ,正方形
,正方形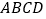 的边长为
的边长为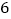 ,点
,点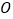 是对角线
是对角线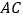 、
、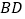 的交点,点
的交点,点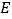 在
在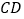 上,过点
上,过点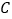 作
作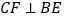 ,垂足为
,垂足为 ,连接
,连接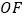 ,
, (1)试利用射影定理证明
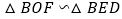 ;
;(2)若
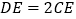 ,求
,求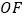 的长.
的长.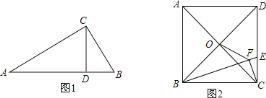
-
科目: 来源: 题型:
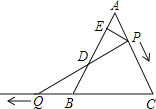
查看答案和解析>>【题目】如图,
 是边长为6的等边三角形,
是边长为6的等边三角形, 是
是 边上一动点,由
边上一动点,由 向
向 运动(与
运动(与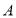 、
、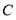 不重合),
不重合),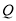 是
是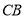 延长线上一动点,与点
延长线上一动点,与点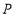 同时以相同的速度由
同时以相同的速度由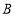 向
向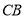 延长线方向运动(
延长线方向运动(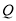 不与
不与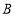 重合),过
重合),过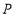 作
作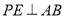 于
于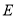 ,连接
,连接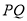 交
交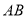 于
于 .
.
(1)当
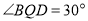 时,求
时,求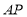 的长;
的长;(2)在运动过程中线段
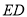 的长是否发生变化?如果不变,求出线段
的长是否发生变化?如果不变,求出线段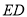 的长;如果发生改变,请说明理由.
的长;如果发生改变,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工程,乙工程队单独先做10天后,再由甲、乙两个工程队合作20天就能完成全部工作,已知甲工程队单独完成此工程所需天数是乙工程队单独完成此工程所需天数的
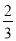 .
.(1)求甲、乙工程队单独完成此工程各需多少天;
(2)甲工程队每天的费用为0.67万元,乙工程每天的费用为0.33万元,该工程的预算费用为20万元,若甲、乙工程队一起合作完成该工程,请问工程费用是否够用?若不够用,应追加多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
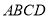 中,
中,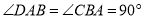 ,将
,将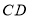 绕点
绕点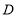 逆时针旋转
逆时针旋转 至
至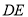 ,连接
,连接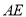 ,若
,若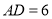 ,
,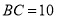 ,则
,则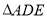 的面积是( )
的面积是( )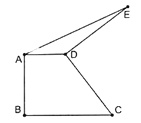
A.
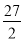 B.12C.9D.8
B.12C.9D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形
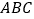 中,
中,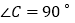 ,
, ,以
,以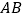 为边作正方形
为边作正方形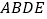 ,连接
,连接 、
、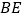 交
交 ,
,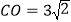 ,则
,则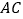 的长为( )
的长为( )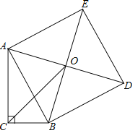
A.
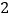 B.
B.  C.
C. 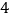 D.
D. 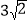
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在
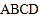 中,
中,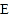 ,
,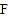 分别是
分别是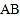 ,
,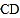 的中点,
的中点,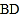 是对角线,
是对角线,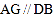 交
交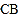 延长线于
延长线于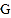 .若四边形
.若四边形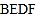 是菱形,则四边形
是菱形,则四边形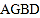 是( )
是( )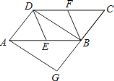
A. 平行四边形 B. 矩形
C. 菱形 D. 正方形
相关试题

