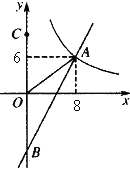
【题目】如图,一次函数y=kx+b的图象分别与反比例函数![]() 的图象在第一象限交于点A(8,6),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(8,6),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和![]() 的表达式;
的表达式;
(2)已知点C(0,10),试在该一次函数图象上确定一点M,使得MB=MC。求此时点M的坐标.
参考答案:
【答案】(1)y=2x-10;(2)M(5,0)
【解析】分析:(1)、根据点A的坐标求出反比例函数的解析式,然后根据OA=OB得出点B的坐标,最后根据点A和点B的坐标求出一次函数的解析式;(2)、根据MB=MC得出点M在线段BC的中垂线上,从而得出点的坐标.
详解:解(1):将A(8,6)代入![]() , 得
, 得![]() ,∴a=48,∴反比例函数为
,∴a=48,∴反比例函数为![]() ,
,
∵OA=10,由于OA=OB,且B在y轴负半轴上,∴B(0,-10)
将A(8,6),B(0,-10)代入y=kx+b
得:![]() ,∴
,∴![]() ,∴y=2x-10
,∴y=2x-10
(2)∵MB=MC,∴M在线段BC的中垂线上,即x轴上,
∴M为一次函数图象与 x轴交点,令2x-10=0,∴x=5,∴M(5,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,直线y=12x+2与
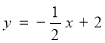 交坐标轴于A,B两点.以AB为斜边在第一象限作等腰直角三角形ABC,C为直角顶点,连接OC.
交坐标轴于A,B两点.以AB为斜边在第一象限作等腰直角三角形ABC,C为直角顶点,连接OC.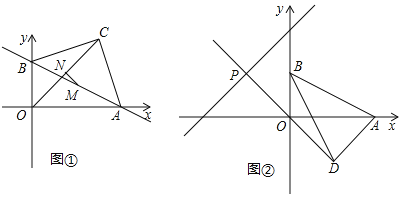
(1)求线段AB的长度
(2)求直线BC的解析式;
(3)如图②,将线段AB绕B点沿顺时针方向旋转至BD,且
 ,直线DO交直线y=x+3
,直线DO交直线y=x+3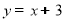 于P点,求P点坐标.
于P点,求P点坐标. -
科目: 来源: 题型:
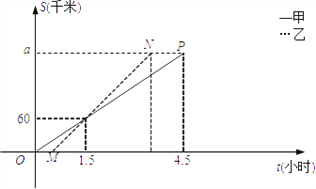
查看答案和解析>>【题目】甲、乙两车从A地将一批物品匀速运往B地,已知甲出发0.5h后乙开始出发,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,请结合图中的信息解决如下问题:
(1)计算甲、乙两车的速度及a的值;
(2)乙车到达B地后以原速立即返回.
①在图中画出乙车在返回过程中离A地的距离S(km)与时间t(h)的函数图象;②请问甲车在离B地多远处与返程中的乙车相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形
 的边长是
的边长是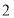 ,
,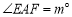 ,将
,将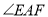 绕点
绕点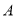 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交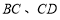 于点
于点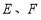 ,
,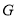 是
是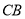 延长线上一点,且始终保持
延长线上一点,且始终保持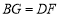 .
.(1)求证:
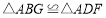 ;
;(2)求证:
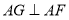 ;
;(3)当
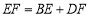 时:
时:①求
 的值;②若
的值;②若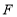 是
是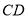 的中点,求
的中点,求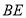 的长.
的长.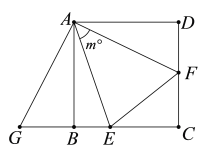
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,PB=PC,给出下面结论:①BP=CP,②EB=EC,③AD⊥BC,④EA平分∠BEC,其中正确的结论有( )
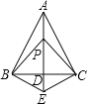
A.①②④B.①③④C.①②③D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B、C、D是直径为AB的⊙O上的四个点,CD=BC,AC与BD交于点E。
(1)求证:DC2=CE·AC;
(2)若AE=2EC,求
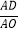 之值;
之值;(3)在(2)的条件下,过点C作⊙O的切线,交AB的延长线于点H,若S△ACH=
 ,求EC之长.
,求EC之长.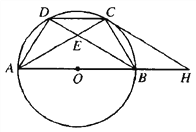
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(5mn2﹣4m2n)(﹣2mn)
(2)(x+7)(x﹣6)﹣(x﹣2)(x+1)
(3) (-
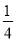 )2 016×161 008;
)2 016×161 008;【答案】(1)﹣10m2n3+8m3n2;(2)2x﹣40;(3)1.
【解析】试题分析:(1)原式利用单项式乘以多项式法则计算即可得到结果;
(2)原式两项利用多项式乘以多项式法则计算,去括号合并即可得到结果;
(3)先根据幂的乘方的逆运算,把(-
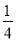 )2 016化为(
)2 016化为(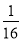 )1008,再根据积的乘方的逆运算计算即可.
)1008,再根据积的乘方的逆运算计算即可.试题解析:(1)原式=(5mn2)(﹣2mn)+(﹣4m2n)(﹣2mn)=﹣10m2n3+8m3n2;
(2)原式=x2﹣6x+7x﹣42﹣x2﹣x+2x+2=2x﹣40.
(3)原式=(
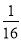 )1008×161 008=(
)1008×161 008=(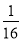 ×16)1 008=1.
×16)1 008=1.【题型】解答题
【结束】
19【题目】如图,方格图中每个小正方形的边长为1,点A、B、C都是格点.
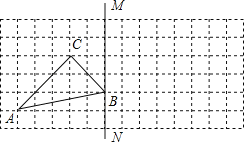
(1)画出△ABC关于直线BM对称的△A1B1C1;
(2)写出AA1的长度.
相关试题

