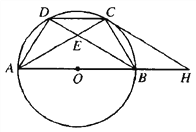
【题目】如图,点A、B、C、D是直径为AB的⊙O上的四个点,CD=BC,AC与BD交于点E。
(1)求证:DC2=CE·AC;
(2)若AE=2EC,求![]() 之值;
之值;
(3)在(2)的条件下,过点C作⊙O的切线,交AB的延长线于点H,若S△ACH=![]() ,求EC之长.
,求EC之长.
参考答案:
【答案】(1)证明见解析;(2)![]() ;(3)EC=2
;(3)EC=2
【解析】分析:(1)、根据题意得出△ACD和△DCE相似即可得出答案;(2)、设EC=k,则AE=2k,根据第一题的结论得出DC的长度,连接OC,OD,根据角平分线得出BD和DC的长度,根据Rt△ABC的性质得出AB的长度,从而得出∠BOD和∠DOA的度数,从而得出AD=AO,得出比值;(3)、设EC=k,根据切线的性质得出CG和AH的长度,最后根据△ACH的面积求出k的值.
详解:(1)证明:∵CD=BC,∴∠DAC=∠CDB,又∵∠ACD=∠DCE,∴△ACD∽△DCE,
∴![]() ,∴DC2=CE·AC;
,∴DC2=CE·AC;
(2)设EC=k,则AE=2k,∴AC=3k,由(1)DC2=CE·AC=3k2,
DC=![]() k,连接OC,OD, ∵CD=BC,∴OC平分∠DOB,∴BC=DC=
k,连接OC,OD, ∵CD=BC,∴OC平分∠DOB,∴BC=DC=![]() k,
k,
∵AB是⊙O的直径,∴在Rt△ACB中,![]() ,
,
∴OB=OC=OD=![]() k,∴∠BOD=120°,∴∠DOA=60°,∴AD=AO,∴
k,∴∠BOD=120°,∴∠DOA=60°,∴AD=AO,∴![]() ;
;
(3)∵CH是⊙O的切线,连接CO,∴OC⊥CH.∵∠COH=60°,∠H=30°,
过C作CG⊥AB于G, 设EC=k,∵∠CAB=30°,∴![]() ,
,
又∵∠H=∠CAB=30°,∴AC=CH=3k,∴AH=![]() ,
,
∵S△ACH=![]() , ∴
, ∴![]() ,∴k2=4,k=2,即EC=2.
,∴k2=4,k=2,即EC=2.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形
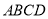 的边长是
的边长是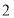 ,
,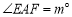 ,将
,将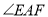 绕点
绕点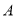 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交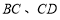 于点
于点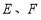 ,
,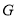 是
是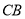 延长线上一点,且始终保持
延长线上一点,且始终保持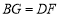 .
.(1)求证:
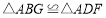 ;
;(2)求证:
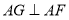 ;
;(3)当
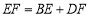 时:
时:①求
 的值;②若
的值;②若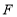 是
是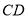 的中点,求
的中点,求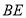 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象分别与反比例函数
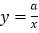 的图象在第一象限交于点A(8,6),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(8,6),与y轴的负半轴交于点B,且OA=OB.(1)求函数y=kx+b和
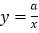 的表达式;
的表达式;(2)已知点C(0,10),试在该一次函数图象上确定一点M,使得MB=MC。求此时点M的坐标.
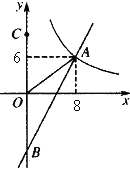
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,PB=PC,给出下面结论:①BP=CP,②EB=EC,③AD⊥BC,④EA平分∠BEC,其中正确的结论有( )
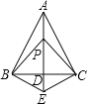
A.①②④B.①③④C.①②③D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(5mn2﹣4m2n)(﹣2mn)
(2)(x+7)(x﹣6)﹣(x﹣2)(x+1)
(3) (-
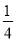 )2 016×161 008;
)2 016×161 008;【答案】(1)﹣10m2n3+8m3n2;(2)2x﹣40;(3)1.
【解析】试题分析:(1)原式利用单项式乘以多项式法则计算即可得到结果;
(2)原式两项利用多项式乘以多项式法则计算,去括号合并即可得到结果;
(3)先根据幂的乘方的逆运算,把(-
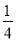 )2 016化为(
)2 016化为(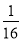 )1008,再根据积的乘方的逆运算计算即可.
)1008,再根据积的乘方的逆运算计算即可.试题解析:(1)原式=(5mn2)(﹣2mn)+(﹣4m2n)(﹣2mn)=﹣10m2n3+8m3n2;
(2)原式=x2﹣6x+7x﹣42﹣x2﹣x+2x+2=2x﹣40.
(3)原式=(
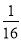 )1008×161 008=(
)1008×161 008=(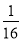 ×16)1 008=1.
×16)1 008=1.【题型】解答题
【结束】
19【题目】如图,方格图中每个小正方形的边长为1,点A、B、C都是格点.
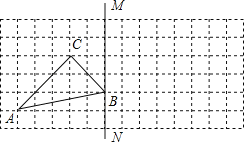
(1)画出△ABC关于直线BM对称的△A1B1C1;
(2)写出AA1的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠C=90°,AC=BC=
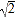 ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )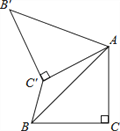
A.
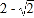 B.
B. 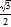 C.
C. 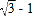 D. 1
D. 1 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织了“健康教育”手抄报征集活动,现从中抽取部分作品,按A、B、C、D四个等级进行奖励,并根据统计结果绘制了如下两幅不完整统计图.
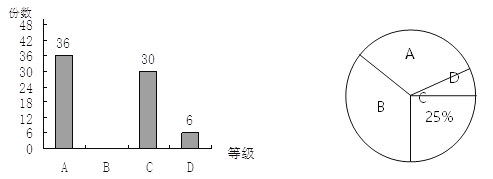
(1)求抽取了多少份作品.
(2)被抽取作品中B等级有多少份?并补全条形统计图.
(3)扇形统计图中D等级所对的圆心角是多少度?
(4)若全校共征集到作品600份,请估计A作品有多少份?
相关试题

