【题目】某校组织了“健康教育”手抄报征集活动,现从中抽取部分作品,按A、B、C、D四个等级进行奖励,并根据统计结果绘制了如下两幅不完整统计图.
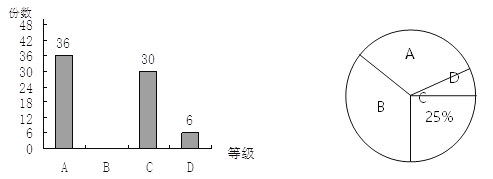
(1)求抽取了多少份作品.
(2)被抽取作品中B等级有多少份?并补全条形统计图.
(3)扇形统计图中D等级所对的圆心角是多少度?
(4)若全校共征集到作品600份,请估计A作品有多少份?
参考答案:
【答案】(1)120(份);(2)48(份),详见解析;(3)18°;(4)180份.
【解析】
(1)用C等级份数除以C等级所占的百分比,可得抽取的数量;
(2)用(1)中所求总份数减去A、C、D三等级数量即可得到B等级作品数,并补全统计图;
(3)先算出D等级所占总数的百分比,再乘以360°,即可算出度数.
(4)利用样本估计总体,将样本中A等级所占比例乘以600,可估计A等级数量.
(1)根据题意,共抽取作品30÷25%=120(份);
(2)B等级作品数为:120﹣36﹣30﹣6=48(份),
补全条形统计图如图所示:
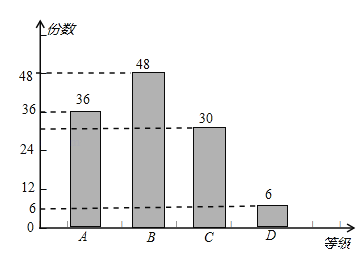
(3)6÷120=5%,360°×5%=18°.
(4)600×![]() =180,
=180,
答:若该校共征集到600份作品,估计等级为A的作品约有180份.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B、C、D是直径为AB的⊙O上的四个点,CD=BC,AC与BD交于点E。
(1)求证:DC2=CE·AC;
(2)若AE=2EC,求
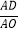 之值;
之值;(3)在(2)的条件下,过点C作⊙O的切线,交AB的延长线于点H,若S△ACH=
 ,求EC之长.
,求EC之长.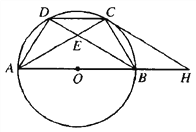
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(5mn2﹣4m2n)(﹣2mn)
(2)(x+7)(x﹣6)﹣(x﹣2)(x+1)
(3) (-
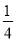 )2 016×161 008;
)2 016×161 008;【答案】(1)﹣10m2n3+8m3n2;(2)2x﹣40;(3)1.
【解析】试题分析:(1)原式利用单项式乘以多项式法则计算即可得到结果;
(2)原式两项利用多项式乘以多项式法则计算,去括号合并即可得到结果;
(3)先根据幂的乘方的逆运算,把(-
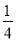 )2 016化为(
)2 016化为(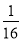 )1008,再根据积的乘方的逆运算计算即可.
)1008,再根据积的乘方的逆运算计算即可.试题解析:(1)原式=(5mn2)(﹣2mn)+(﹣4m2n)(﹣2mn)=﹣10m2n3+8m3n2;
(2)原式=x2﹣6x+7x﹣42﹣x2﹣x+2x+2=2x﹣40.
(3)原式=(
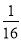 )1008×161 008=(
)1008×161 008=(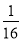 ×16)1 008=1.
×16)1 008=1.【题型】解答题
【结束】
19【题目】如图,方格图中每个小正方形的边长为1,点A、B、C都是格点.
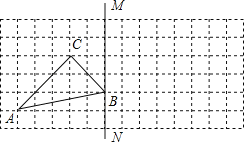
(1)画出△ABC关于直线BM对称的△A1B1C1;
(2)写出AA1的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠C=90°,AC=BC=
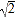 ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( )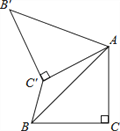
A.
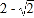 B.
B. 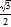 C.
C. 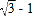 D. 1
D. 1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为________.
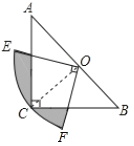
-
科目: 来源: 题型:
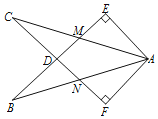
查看答案和解析>>【题目】如图,在Rt△AEB和Rt△AFC中,∠E=∠F=90°,BE=CF.BE与AC相交于点M,与CF相交于点D,AB与CF相交于点N,∠EAC=∠FAB.有下列结论:①∠B=∠C;②CD=DN;③CM=BN;④△ACN≌△ABM.其中正确结论的序号是________.
-
科目: 来源: 题型:
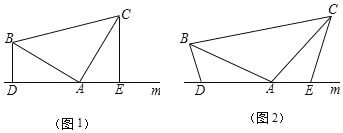
查看答案和解析>>【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,证明:△ABD≌△ACE,DE=BD+CE;
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D, A, E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=a,其中a为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
相关试题

