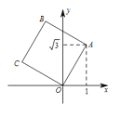
【题目】如图,将正方形OABC放在平面直角坐标系xOy中,O是原点,若点A的坐标为(1,![]() ),则点C的坐标( )
),则点C的坐标( )
A.(-1,![]() )B.(
)B.(![]() )C.
)C.![]() D.(-2,1)
D.(-2,1)
参考答案:
【答案】B
【解析】
作AD⊥轴于D,作CE⊥x轴于E,则∠ADO=∠OEC=90°,得出∠1+∠2=90°,由正方形的性质得出OC=AO,∠1+∠3=90°,证出∠3=∠2,由AAS证明△OCE≌△AOD,OE=AD=![]() ,CE=OD=1,即可得出结果.
,CE=OD=1,即可得出结果.
解:作AD⊥轴于D,作CE⊥x轴于E,如图所示:
则∠ADO=∠OEC=90°,
∴∠1+∠2=90°,
∵点A的坐标为(1,![]() ),
),
∴OD=1,AD=![]() ,
,
∵四边形OABC是正方形,
∴∠AOC=90°,OC=AO,
∴∠1+∠3=90°,
∴∠3=∠2,
在△OCE和△AOD中,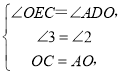 ,
,
∴△OCE≌△AOD(AAS),
∴OE=AD=![]() ,CE=OD=1,
,CE=OD=1,
∴点C的坐标为(-![]() ,1);
,1);
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,直线y=kx+x+1过一定点A,坐标系中有点B(2,0)和点C,要使以A、O、B、C为顶点的四边形为平行四边形,则点C的坐标为
-
科目: 来源: 题型:
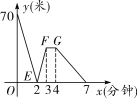
查看答案和解析>>【题目】(2016齐齐哈尔)有一科技小组进行机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上.甲、乙两机器人分别从A、B两点同时同向出发,历时7分钟同时到达C点,乙机器人始终以60米/分的速度行走.如图是甲、乙两机器人之间的距离y(米)与它们的行走时间x(分钟)之间的函数图象,请结合图象,回答下列问题:
(1)A、B两点之间的距离是________米,甲机器人前2分钟的速度为______米/分;
(2)若前3分钟甲机器人的速度不变,求线段EF所在直线的函数解析式;
(3)若线段
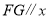 轴,则此段时间,甲机器人的速度为________米/分;
轴,则此段时间,甲机器人的速度为________米/分;(4)求A、C两点之间的距离;
(5)直接写出两机器人出发多长时间相距28米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点 A、B 在数轴上分别表示有理数 a、b.
(1)对照数轴,填写下表:

(2)若 A、B 两点间的距离记为 d,试问 d 和 a、b(a<b)有何数量关系?数学式子表示.
(3)求所有到数 5 和-5 的距离之和为 10 的整数的和,列式计算.
(4)若点 C 表示的数为 x,当点 C 在什么位置时,|x+1|+|x﹣2|取得的值最小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD的边长为2,正方形内有一动点P,求点P到三个顶点A、B、C的距离之和的最小值( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在菱形ABCD中,AB=4,∠BAD=120,△ABF为等边三角形;点E.F分别在菱形的边BC.CD上滑动,且点E.F不与点B.C.D重合,当点E.F分别在BC.CD上滑动时,求四边形ABCF的面积= ___________并求△CEF面积的最大值___________

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的一元二次方程
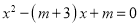
(1)求证:无论m取什么实数值,方程总有两个不相等的实数根;
(2)若
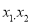 是原方程的两个实数根,且满足
是原方程的两个实数根,且满足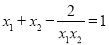 ,求m的值
,求m的值
相关试题

