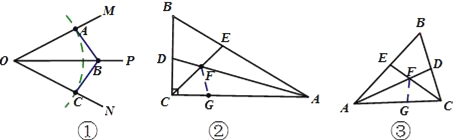
【题目】(1)如图①,OP是∠MON的平分线,点A为OM上一点,点B为OP上一点.请你利用该图形在ON上找一点C,使△COB≌△AOB,请在图①画出图形.参考这个作全等三角形的方法,解答下列问题:
(2)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你写出FE与FD之间的数量关系,并说明理由;
(3)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,在(2)中所得结论是否仍然成立?请你直接作出判断,不必说明理由.

参考答案:
【答案】(1)画图见解析;(2)DF=EF,理由见解析;(3)DF=EF 仍然成立,理由见解析.
【解析】(1)在∠MON的两边上以O为端点截取相等的两条相等的线段,两个端点与角平分线上任意一点相连,所构成的两个三角形全等,即△COB≌△AOB;
(2)根据图(1)的作法,在CG上截取CG=CD,证得△CFG≌△CFD(SAS),得出DF=GF;再根据ASA证明△AFG≌△AFE,得EF=FG,故得出EF=FD;
(3)根据图(1)的作法,在CG上截取AG=AE,证得△EAF≌△GAF(SAS),得出FE=FG;再根据ASA证明△FDC≌△FGC,得DF=FG,故得出EF=FD.
解:(1)如图①所示,△COB≌△AOB,点C即为所求.
(2)如图②,在CG上截取CG=CD,
∵CE是∠BCA的平分线,
∴∠DCF=∠GCF,
在△CFG和△CFD中,
CG=CD,∠DCF=∠GCF,CF=CF,
∴△CFG≌△CFD(SAS),
∴DF=GF.
∵∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,
∴∠FAC=![]() ∠BAC,∠FCA=
∠BAC,∠FCA=![]() ∠ACB,且∠EAF=∠GAF,
∠ACB,且∠EAF=∠GAF,
∴∠FAC+∠FCA=![]() (∠BAC+∠ACB)=
(∠BAC+∠ACB)=![]() =60°,
=60°,
∴∠AFC=120°,
∴∠CFD=60°=∠CFG,
∴∠AFG=60°,
又∵∠AFE=∠CFD=60°,
∴∠AFE=∠AFG,
在△AFG和△AFE中,
∠AFE=∠AFG,AF=AF,∠EAF=∠GAF,
∴△AFG≌△AFE(ASA),
∴EF=GF,
∴DF=EF;
(3)DF=EF 仍然成立.
证明:如图③,在CG上截取AG=AE,
同(2)可得△EAF≌△GAF(SAS),
∴FE=FG,∠EFA=∠GFA.
又由题可知,∠FAC=![]() ∠BAC,∠FCA=
∠BAC,∠FCA=![]() ∠ACB,
∠ACB,
∴∠FAC+∠FCA=![]() (∠BAC+∠ACB)=60°,
(∠BAC+∠ACB)=60°,
∴∠AFC=180°﹣(∠FAC+∠FCA)=120°,
∴∠EFA=∠GFA=180°﹣120°=60°=∠DFC,
∴∠CFG=∠CFD=60°,
同(2)可得△FDC≌△FGC(ASA),
∴FD=FG,
∴FE=FD.
“点睛”此题主要考查全等三角形的判定和性质的运用,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具,在判定三角形全等时,关键是选择恰当的判定条件,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造全等三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x≠0时,下列运算不正确的是( )
A.a2a=a3
B.(﹣a3)2=a6
C.(3a2)2=9a4
D.a3÷a3=a -
科目: 来源: 题型:
查看答案和解析>>【题目】任何一个凸多边形的外角和等于____.它与该多边形的__无关.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校就“遇见老人摔倒后如何处理”的问题,随机抽取该校部分学生进行问卷调查(每个被调查的学生必须选择而且只能在4种方式中选择一项),图1和图2是整理数据后绘制的两幅不完整的统计图,请根据图中提供的信息,解答下列问题:
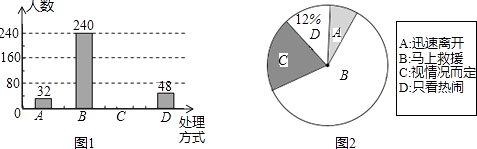
(1)该校随机抽查了名学生;
(2)将图1补充完整,在图2中,“视情况而定”部分所占的圆心角是度;
(3)估计该校2800名学生中采取“马上救助”的方式的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC经过平移后,使点A与点A′(﹣1,4)重合.
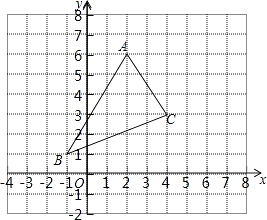
(1)画出平移后的△A′B′C′;
(2)求出△A′B′C′的面积;
(3)若三角形ABC内有一点P(a,b),经过平移后的对应点P′的坐标;
(4)若连接AA′,CC′,则这两条线段之间的关系是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC中,∠A=90°,BC的垂直平分线DE交BC于点E,交AC于点D.
(1)若∠C=35°,求∠DBA的度数;
(2)若△ABD的周长为30,AC=18,求AB的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题错误的是( )
A. 平分弦的直径垂直于弦
B. 三角形一定有外接圆和内切圆
C. 等弧对等弦
D. 经过切点且垂直于切线的直线必经过圆心
相关试题

