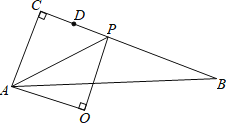
【题目】如图,Rt△ABC中,∠C=90°,AC=2,BC=5,点D是BC边上一点且CD=1,点P是线段DB上一动点,连接AP,以AP为斜边在AP的下方作等腰Rt△AOP.当P从点D出发运动至点B停止时,点O的运动路径长为_____.
参考答案:
【答案】2![]()
【解析】过O点作OE⊥CA于E,OF⊥BC于F,连接CO,如图,易得四边形OECF为矩形,由△AOP为等腰直角三角形得到OA=OP,∠AOP=90°,则可证明△OAE≌△OPF,所以AE=PF,OE=OF,根据角平分线的性质定理的逆定理得到CO平分∠ACP,从而可判断当P从点D出发运动至点B停止时,点O的运动路径为一条线段,接着证明CE=![]() (AC+CP),然后分别计算P点在D点和B点时OC的长,从而计算它们的差即可得到P从点D出发运动至点B停止时,点O的运动路径长.
(AC+CP),然后分别计算P点在D点和B点时OC的长,从而计算它们的差即可得到P从点D出发运动至点B停止时,点O的运动路径长.
过O点作OE⊥CA于E,OF⊥BC于F,连接CO,如图,

∵△AOP为等腰直角三角形,
∴OA=OP,∠AOP=90°,
易得四边形OECF为矩形,
∴∠EOF=90°,CE=CF,
∴∠AOE=∠POF,
∴△OAE≌△OPF,
∴AE=PF,OE=OF,
∴CO平分∠ACP,
∴当P从点D出发运动至点B停止时,点O的运动路径为一条线段,
∵AE=PF,
即AC-CE=CF-CP,
而CE=CF,
∴CE=![]() (AC+CP),
(AC+CP),
∴OC=![]() CE=
CE=![]() (AC+CP),
(AC+CP),
当AC=2,CP=CD=1时,OC=![]() ×(2+1)=
×(2+1)=![]() ,
,
当AC=2,CP=CB=5时,OC=![]() ×(2+5)=
×(2+5)=![]() ,
,
∴当P从点D出发运动至点B停止时,点O的运动路径长=![]() -
-![]() =2
=2![]() .
.
故答案为2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用火柴按下列方式摆出图形:
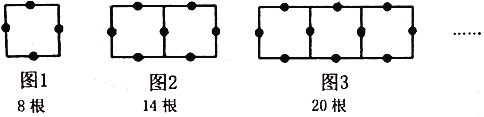
(1)第
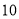 个图形需要多少根火柴?
个图形需要多少根火柴?(2)按这样摆下去,第
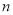 个图形需要多少根火柴?
个图形需要多少根火柴?(3)用
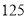 根火柴能摆出第
根火柴能摆出第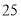 个图形吗?
个图形吗? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE﹣ED﹣DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒.设P、Q同发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(曲线OM为抛物线的一部分),则下列结论:①AD=BE=5;②cos∠ABE=
 ;③当0<t≤5时,y=
;③当0<t≤5时,y= t2;④当t=
t2;④当t=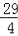 秒时,△ABE∽△QBP;其中正确的结论是 (填序号).
秒时,△ABE∽△QBP;其中正确的结论是 (填序号).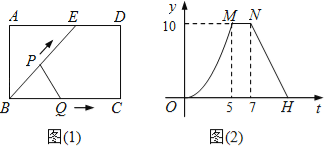
-
科目: 来源: 题型:
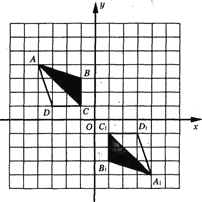
查看答案和解析>>【题目】如图,在网格中、建立了平面直角坐标系,每个小正方形的边长均为1个单位长度,将四边形ABCD 绕坐标原点O按顺时针方向旋转180°后得到四边形A1B1C1D1.
(1)直接写出点D1的坐标________,点D旋转到点D1所经过的路线长_______;
(2)请你在△ACD的三个内角中任选一个锐角,若你所选的锐角是________,则它所对应的正弦函数值是_________;
(3)将四边形A1B1C1D1平移,得到四边形A2B2C2D2,若点D2(4,5),画出平移后的图形.
-
科目: 来源: 题型:
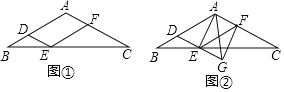
查看答案和解析>>【题目】如图①,在△ABC中,AB=AC,过AB上一点D作DE∥AC交BC于点E,以E为顶点,ED为一边,作∠DEF=∠A,另一边EF交AC于点F.
(1)求证:四边形ADEF为平行四边形;
(2)当点D为AB中点时,判断ADEF的形状;
(3)延长图①中的DE到点G,使EG=DE,连接AE,AG,FG,得到图②,若AD=AG,判断四边形AEGF的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分) 2011年5月上旬,无锡市共有35000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩,从某校随机抽取了50名男生的测试成绩,根
据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D
表示)四个等级进行统计,并绘制成如图所示的扇形图和统计表:
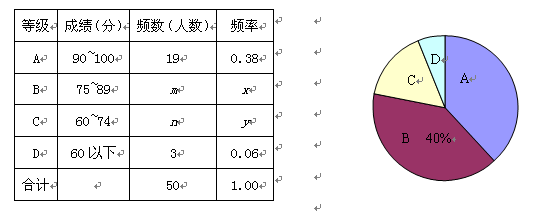
请你根据以上图表提供的信息,解答下列问题:
【1】(1) m= ,n= ,x= ,y= ;
【2】(2)在扇形图中,C等级所对应的圆心角是 度;
【3】(3)如果该校九年级共有500名男生参加了立定跳远测试,那么请你估计这些男生成绩等级达到优秀和良好的共有多少人?
-
科目: 来源: 题型:
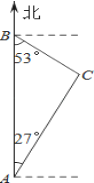
查看答案和解析>>【题目】如图,禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处距离为99海里,可疑船只正沿南偏东53°方向航行.我渔政船迅速沿北偏东27°方向前去拦截,2小时后刚好在C处将可疑船只拦截.求该可疑船只航行的速度.
(参考数据:sin27°≈
 , cos27°≈
, cos27°≈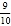 , tan27°≈
, tan27°≈ , sin53°≈
, sin53°≈ , cos53°≈
, cos53°≈ , tan53°≈
, tan53°≈ )
)
相关试题

