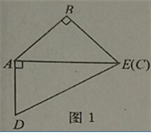
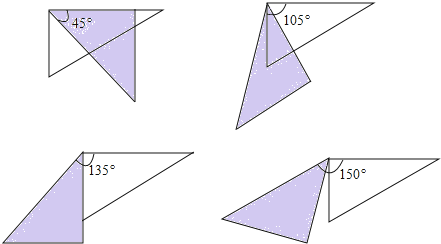
【题目】如图,取一副三角板按图1拼接,固定三角板ADE(含30°),将三角板ABC(含45°)绕点A顺时针方向旋转一个大小为α的角(0°<α≤45°),试问:
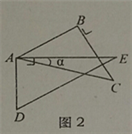
(1)当∠α=_____度时,能使图2中的AB∥DE;
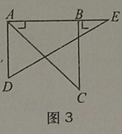
(2)当旋转到AB与AE重叠时(如图3),则∠α=_____度;
(3)当△ADE的一边与△ABC的某一边平行(不共线)时,直接写出旋转角α的所有可能的度数;
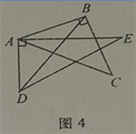
(4)当0°<α≤45°时,连接BD(如图4),探求∠DBC+∠CAE+∠BDE的值的大小变化情况,并说明理由.
参考答案:
【答案】 15° 45°(3) 15°,45°,105°,135°,150° (4) 保持不变;理由见解析
【解析】试题分析: (1)根据平行线的性质,可得∠BAE=∠E=30°,再根据∠BAC=45°,即可得出∠CAE=45°-30°=15°;
(2)根据当旋转到AB与AE重叠时,∠α=∠BAC即可得到结果;
(3)要分5种情况进行讨论:AD∥BC、DE∥AB、DE∥BC、DE∥AC、AE∥BC,分别画出图形,计算出度数即可;
(4)先设BD分别交AC、AE于点M、N,在△AMN中,∠AMN+∠CAE+∠ANM=180,再根据∠ANM=∠E+∠BDE,∠AMN=∠C+∠DBC,得出∠E+∠BDE+∠CAE+∠C+∠DBC=180°,然后根据∠C=30°,∠E=45°,即可得出∠BDE+∠CAE+∠DBC的度数.
试题解析:
(1)如图2,当AB∥DE时,∠BAE=∠E=30°,
∵∠BAC=45°,
∴∠CAE=45°-30°=15°,
即∠α=15°,
故答案为:15;
(2)当旋转到AB与AE重叠时,∠α=∠BAC=45°,
故答案为:45;
(3)当△ADE的一边与△ABC的某一边平行(不共线)时,旋转角α的所有可能的度数是:15°,45°,105°,135°,150°;
(4)当0°<α<45°,∠BDE+∠CAE+∠DBC=105°,保持不变;理由如下:
设BD分别交AC、AE于点M、N,
在△AMN中,∠AMN+∠CAE+∠ANM=180,
∵∠ANM=∠E+∠BDE,∠AMN=∠C+∠DBC,
∴∠E+∠BDE+∠CAE+∠C+∠DBC=180°,
∵∠C=30°,∠E=45°,
∴∠BDE+∠CAE+∠DBC=105°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个数的平方根与它的立方根相同,那么这个数是( )
A.±1 B.0 C.1 D.0和1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个数的平方根等于这个数的立方根,那么这个数是__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣2x+k=0有实数根,则k的取值范围是_____.
-
科目: 来源: 题型:
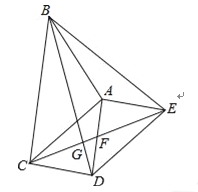
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=
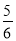 ,OC=
,OC= ,则另一直角边BC的长为__________.
,则另一直角边BC的长为__________.
-
科目: 来源: 题型:
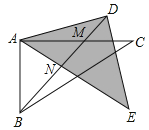
查看答案和解析>>【题目】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE.下列结论中:
①CE=BD;
②△ADC是等腰直角三角形;
③∠ADB=∠AEB;
④CDAE=EFCG;
一定正确的结论有( )
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果x2=49,那么x等于( )
A. 7 B. ﹣7 C. 7或﹣7 D. 49或﹣49
相关试题

