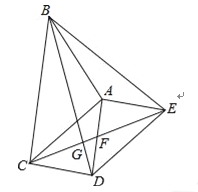
【题目】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE.下列结论中:
①CE=BD;
②△ADC是等腰直角三角形;
③∠ADB=∠AEB;
④CDAE=EFCG;
一定正确的结论有( )
A.1个 B.2个 C.3个 D.4个
参考答案:
【答案】D
【解析】
试题分析:①∵∠BAC=∠DAE=90°,
∴∠BAC+∠DAC=∠DAE+∠DAC,
即:∠BAD=∠CAE,
∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AE=AD,
∴△BAD≌△CAE(SAS),
∴CE=BD,
∴故①正确;
②∵四边形ACDE是平行四边形,
∴∠EAD=∠ADC=90°,AE=CD,
∵△ADE是等腰直角三角形,
∴AE=AD,
∴AD=CD,
∴△ADC是等腰直角三角形,
∴②正确;
③∵△ADC是等腰直角三角形,
∴∠CAD=45°,
∴∠BAD=90°+45°=135°,
∵∠EAD=∠BAC=90°,∠CAD=45°,
∴∠BAE=360°﹣90°﹣90°﹣45°=135°,
又AB=AB,AD=AE,
∴△BAE≌△BAD(SAS),
∴∠ADB=∠AEB;
故③正确;
④∵△BAD≌△CAE,△BAE≌△BAD,
∴△CAE≌△BAE,
∴∠BEA=∠CEA=∠BDA,
∵∠AEF+∠AFE=90°,
∴∠AFE+∠BEA=90°,
∵∠GFD=∠AFE,∠ADB=∠AEB,
∴∠ADB+∠GFD=90°,
∴∠CGD=90°,
∵∠FAE=90°,∠GCD=∠AEF,
∴△CGD∽△EAF,
∴![]() ,
,
∴CDAE=EFCG.
故④正确,
故正确的有4个.
故选:D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣2x+k=0有实数根,则k的取值范围是_____.
-
科目: 来源: 题型:
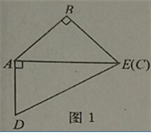
查看答案和解析>>【题目】如图,取一副三角板按图1拼接,固定三角板ADE(含30°),将三角板ABC(含45°)绕点A顺时针方向旋转一个大小为α的角(0°<α≤45°),试问:
(1)当∠α=_____度时,能使图2中的AB∥DE;
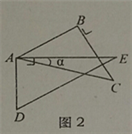
(2)当旋转到AB与AE重叠时(如图3),则∠α=_____度;
(3)当△ADE的一边与△ABC的某一边平行(不共线)时,直接写出旋转角α的所有可能的度数;
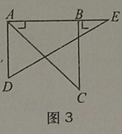
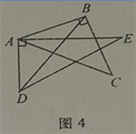
(4)当0°<α≤45°时,连接BD(如图4),探求∠DBC+∠CAE+∠BDE的值的大小变化情况,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=
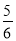 ,OC=
,OC= ,则另一直角边BC的长为__________.
,则另一直角边BC的长为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果x2=49,那么x等于( )
A. 7 B. ﹣7 C. 7或﹣7 D. 49或﹣49
-
科目: 来源: 题型:
查看答案和解析>>【题目】求x的值:4x2﹣49=0;
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.3x-2x=x
B.2x3x=6x
C.(2x)2=4x
D.6x÷2x=3x
相关试题

