【题目】某商场销售一批名牌衬衣,平均每天可售出20件,每件衬衣盈利40元.为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衣降价1元,商场平均每天可多售出2件.
(1)若商场平均每天盈利1200元,每件衬衣应降价多少元?
(2)若要使商场平均每天的盈利最多,请你为商场设计降价方案.
参考答案:
【答案】
(1)解:设每件衬衣应降价x元:
(40-x)(20+2x)=1200,
解得 ![]() =20,
=20, ![]() =10(依题意,舍去)
=10(依题意,舍去)
故每件衬衣应降价20元。
(2)解:设总利润为w,则W=(40-x)(20+2x)=-2 ![]() +1250
+1250
∵顶点坐标为(15,1250)
∴当x=15时商场平均每天的盈利最多,最多为1250元
【解析】(1)抓住已知条件商场平均每天盈利1200元,得出此题的等量关系:降价后 每一件的利润![]() 销售量=1200,设未知数建立方程,求出方程的解,再根据扩大销售,增加盈利,尽快减少库存进行取值,即可求出结果。
销售量=1200,设未知数建立方程,求出方程的解,再根据扩大销售,增加盈利,尽快减少库存进行取值,即可求出结果。
(2)设总利润为w,根据w=降价后每一件的利润![]() 降价后的销售量,建立w关于x的函数解析式,再求出其顶点坐标,即可求出每天盈利最多时的降价方案。
降价后的销售量,建立w关于x的函数解析式,再求出其顶点坐标,即可求出每天盈利最多时的降价方案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两人以相同路线前往距离单位10
 的培训中心参加学习.图中
的培训中心参加学习.图中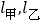 分别表示甲,乙两人前往目的地所走的路程s
分别表示甲,乙两人前往目的地所走的路程s 随时间(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8
随时间(分)变化的函数图象.以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了8 后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )
后遇到甲;④乙出发6分钟后追上甲.其中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y是x的一次函数,当x=1时,y=1;当x=-2时,y=-14.
(1)求这个一次函数的关系式;
(2)在如图所示的平面直角坐标系中作出函数的图像;
(3)由图像观察,当0≤x≤2时,函数y的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两同学用一副扑克牌中牌面数字分别是3,4,5,6的4张牌做抽数字游戏,游戏规则是:将这4张牌的正面全部朝下,洗匀,从中随机抽取一张,抽得的数作为十位上的数字,抽出的牌不放回,然后将剩下的牌洗匀,再从中随机抽取一张,抽得的数作为个位上的数字,这样就得到一个两位数,若这个两位数小于45,则甲获胜,否则乙获胜.你认为这个游戏公平吗?请利用树状图或列表法说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使AB=AC,连结AC,过点D作DE⊥AC,垂足为E.
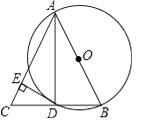
(1)求证:DC=BD;
(2)求证:DE为⊙O的切线. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.

(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列全国各地地铁标志图中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
相关试题

