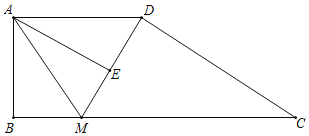
【题目】已知,梯形ABCD中,AD∥BC,∠ABC=90°,AB=3,BC=10,AD=5,M是BC边上的任意一点,联结DM,联结AM.
(1)若AM平分∠BMD,求BM的长;
(2)过点A作AE⊥DM,交DM所在直线于点E.
①设BM=x,AE=y求y关于x的函数关系式;
②联结BE,当△ABE是以AE为腰的等腰三角形时,请直接写出BM的长.
参考答案:
【答案】(1)1或9;(2)①y=![]() .②1或9或4.
.②1或9或4.
【解析】
(1)考虑∠DMB为锐角和钝角两种情况即可解答;
(2) ①作MH⊥AD于H,根据勾股定理,用被开方式含x的二次根式表示DM,根据△ADM面积的两种算法建立等式,即可求出y关于x的函数关系式;②分AB=AE和EA=EB两种情况讨论求解.
解:(1)如图1中,作DH⊥BC于H.则四边形ABHD是矩形,AD=BH=5,AB=DH=3.

当MA平分∠DMB时,易证∠AMB=∠AMD=∠DAM,可得DA=DM=5,
在Rt△DMH中,DM=AD=5,DH=3,
∴MH=![]() =
=![]() =4,
=4,
∴BM=BH-MH=1,
当AM′平分∠BM′D时,同法可证:DA=DM′,HM′=4,
∴BM′=BH+HM′=9.
综上所述,满足条件的BM的值为1或9.
(2)①如图2中,作MH⊥AD于H.

在Rt△DMH中,DM=![]() =
=![]() ,
,
∵S△ADM=![]() ADMH=
ADMH=![]() DMAE,
DMAE,
∴5×3=y![]()
∴y=![]() .
.
②如图3中,当AB=AE时,y=3,此时5×3=3![]() ,
,
解得x=1或9.

如图4中,当EA=EB时,DE=EM,
∵AE⊥DM,
∴DA=AM=5,
在Rt△ABM中,BM=![]() =4.
=4.

综上所述,满足条件的BM的值为1或9或4.
故答案为:(1)1或9;(2)①y=![]() .②1或9或4.
.②1或9或4.
-
科目: 来源: 题型:
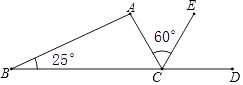
查看答案和解析>>【题目】如图,CE是△ABC的外角∠ACD的平分线,若∠B=25°,∠ACE=60°,则∠A=( )
A.105°
B.95°
C.85°
D.25° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=2x+4的图象与x,y轴分别相交于点A,B,以AB为边作正方形ABCD(点D落在第四象限).
(1)求点A,B,D的坐标;
(2)联结OC,设正方形的边CD与x相交于点E,点M在x轴上,如果△ADE与△COM全等,求点M的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,F是
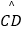 上一点,且
上一点,且 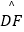 =
=  ,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=110°,∠BAC=20°,则∠E的度数为( )
,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=110°,∠BAC=20°,则∠E的度数为( ) 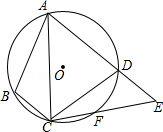
A.60°
B.55°
C.50°
D.45° -
科目: 来源: 题型:
查看答案和解析>>【题目】若直线l1经过点(0,4),l2经过(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为
A. (-2,0) B. (2,0) C. (-6,0) D. (6,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=ax+b和反比例函数y=
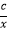 在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( ) 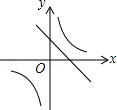
A.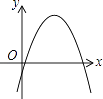
B.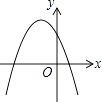
C.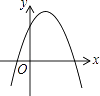
D.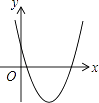
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角. 其中正确的是 (填序号).

相关试题

