【题目】乘法公式的探究及应用.
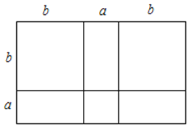
数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形,并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积.
方法1:______;方法2:______.
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系.______;
(3)类似的,请你用图1中的三种纸片拼一个图形验证:
(a+b)(a+2b)=a2+3ab+2b2
(4)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(x-2016)2+(x-2018)2=34,求(x-2017)2的值.

参考答案:
【答案】(1) (a+b)2;a2+b2+2ab;(2)(a+b)2=a2+2ab+b2;(3)见解析;(4)①7;②16.
【解析】
(1)第一种方法:直接用正方形的面积公式求解;第二种方法将其看做是一个两个正方形和两个长方形,分别求出面积再求和即可.
(2)依据(1)中的代数式,即可得到所求的关系;
(3)画出长为a+2b,宽为a+b的长方形,即可完成验证;
(4)①依据a+b=5,可得(a+b)2=25,进而得出a2+b2+2ab=25,再将a2+b2=11,即可得到ab=7;②设x-2017=a,则x-2016=a+1,x-2018=a-1,依据(x-2016)2+(x-2018)2=34,即可得到∴(a+1)2+(a-1)2=34,然后化简得a2=16,即可完成解答.
解:(1)图2大正方形的面积=(a+b)2;图2大正方形的面积=a2+b2+2ab;
故答案为:(a+b)2;a2+b2+2ab;
(2)由题可得(a+b)2,a2+b2,ab之间的等量关系为:(a+b)2=a2+2ab+b2;
故答案为:(a+b)2=a2+2ab+b2;
(3)如图所示,
(4)①∵a+b=5,
∴(a+b)2=25,即a2+b2+2ab=25,
又∵a2+b2=11,
∴ab=7;
②设x-2017=a,则x-2016=a+1,x-2018=a-1,
∵(x-2016)2+(x-2018)2=34,
∴(a+1)2+(a-1)2=34,
∴a2+2a+1+a2-2a+1=34,
∴2a2+2=34,
∴2a2=32,
∴a2=16,
即(x-2017)2=16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据直尺和三角尺的实物摆放图,解决下列问题.



(1)如图1,是我们学过的用直尺和三角尺画平行线的方法的示意图,画图的原理是__________;
(2)如图2,图中互余的角有________________,若要使直尺的边缘DE与三角尺的AB边平行,则应满足_________(填角相等);
(3)如图3,若BC∥GH,试判断AC和FG的位置关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】市实验中学学生会准备调查七年级学生参加“球类”“书画类”“棋牌类:”“器乐类”四类校本课程的人数.
(1)确定调查方式时,甲同学说:“我到七年级(1)班去调查全体同学”;乙同学说:“放学时,我到校门口随机调查部分同学”;丙同学说:“我到七年级每个班随机调查一定数量的同学”.这三位同学的调查方式中,最合理的是______(填“甲”“乙”或“丙”)同学的调查方式.
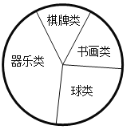
(2)他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图,请你根据图表提供的信息解答下列问题:
①a=________,b=________;
②在扇形统计图中,器乐类所对应的圆心角的度数是________;
③若该校七年级有学生660人,请你估计大约有多少学生参加球类校本课程?
类别
频数(人数)
百分比
球类
25
书画类
20
20%
棋牌类
15
b
器乐类
合计
a
100%
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
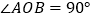 ,线段
,线段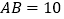 ,若点A在y轴上滑动,点B随着线段AB在射线x轴上滑动,(A、B与O不重合),Rt△AOB的内切⊙K分别与OA、OB、AB切于E、F、P.
,若点A在y轴上滑动,点B随着线段AB在射线x轴上滑动,(A、B与O不重合),Rt△AOB的内切⊙K分别与OA、OB、AB切于E、F、P.(1)在上述变化过程中:Rt△AOB的周长,⊙K的半径,△AOB外接圆半径,这几个量中不会发生变化的是什么?并简要说明理由;
(2)当
 时,求⊙K的半径r;
时,求⊙K的半径r;
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料并把解答过程补充完整.
问题:在关于x,y的二元一次方程组
 中,x>1,y<0,求a的取值范围.
中,x>1,y<0,求a的取值范围.在关于x,y的二元一次方程组中,利用参数a的代数式表示x,y,然后根据x>1,y<0列出关于参数a的不等式组即可求得a的取值范围.
解:由
 ,解得
,解得 ,又因为x>1,y<0,所以
,又因为x>1,y<0,所以 ,解得________.
,解得________.请你按照上述方法,完成下列问题:
已知x-y=4,x>3,y<1,求x+y的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,AC=FC.
(1)求证:AC是⊙O的切线;
(2)已知圆的半径R=5,EF=3,求DF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,等边△ABC中,点D、E分别在BC、AC上,BD=CE,连AD、BE.
(1)求证:△CAD≌△ABE;
(2)如图2,延长FE至点G,使得FG=FA,连AG,试判断△AFG的形状,并说明理由;
(3)在(2)的条件下,连CF,若CF⊥AD,求证:CF⊥CG.

相关试题

