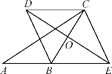
【题目】已知:如图,在△ABC中,O是边BC的中点,E是线段AB延长线上一点,过点C作CD∥BE,交线段EO的延长线于点D,连接BD,CE.
(1)求证:CD=BE;
(2)如果∠ABD=2∠BED,求证:四边形BECD是菱形.
参考答案:
【答案】见解析
【解析】
(1)可通过全等三角形来证明简单的线段相等,△COD和△BOE中,已知了CO=BO,∠COD=∠BOE,CD∥BE,因此不难得出两三角形全等,进而可得出CD=BE.
(2)需先证明四边形AFCE是平行四边形,那么邻边相等的平行四边形是菱形.
(1)∵CD∥BE,
∴∠CDE=∠DEB.
∵O是边BC的中点,
∴CO=BO.
在△COD和△BOE中,

∴△COD≌△BOE(AAS).
∴CD=BE.
(2)∵CD∥BE,CD=BE,
∴四边形BECD是平行四边形.
∵∠ABD=2∠BED,∠ABD=∠BED+∠BDE,
∴∠BED=∠BDE.
∴BD=BE.
∴四边形BECD是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以线段AC的两个端点A,C为圆心,大于
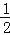 AC的长为半径画弧,两弧相交于B,D两点,连接BD,AB,BC,CD,DA,以下结论:
AC的长为半径画弧,两弧相交于B,D两点,连接BD,AB,BC,CD,DA,以下结论:①BD垂直平分AC;
②AC平分∠BAD;
③AC=BD;
④四边形ABCD是中心对称图形.
其中正确的有( )
A. ①②③ B. ①③④ C. ①②④ D. ②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,曲线AB是顶点为B,与y轴交于点A的抛物线y=﹣x2+4x+2的一部分,曲线BC是双曲线y=
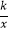 的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2017,m)与Q(2025,n)均在该波浪线上,过点P、Q分别作x轴的垂线,垂足为M、N,连结PQ,则四边形PMNQ的面积为( )
的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2017,m)与Q(2025,n)均在该波浪线上,过点P、Q分别作x轴的垂线,垂足为M、N,连结PQ,则四边形PMNQ的面积为( ) 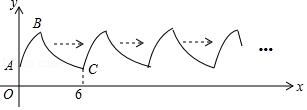
A.72
B.36
C.16
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,若AC⊥BD,且AC≠BD,则四边形EFGH的形状是 .(填“梯形”、“矩形”或“菱形”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,AD是△ABC的一条角平分线,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.
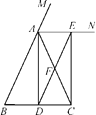
(1)求证:四边形ADCE为矩形;
(2)连接DE,交AC于点F,请判断四边形ABDE的形状,并证明;
(3)线段DF与AB有怎样的关系?请直接写出你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在长方形ABCD中,点P是CD中点,点Q从点A开始,沿着A→B→C→P的路线匀速运动,设△APQ的面积是y,点Q经过的路线长度为x,图2坐标系中折线OEFG表示y与x之间的函数关系,点E的坐标为(4,6),则点G的坐标是_____.
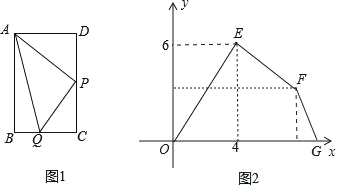
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.请你认真阅读下面关于这个图的探究片段,完成所提出的问题.
(1)探究1:小强看到图(*)后,很快发现AE=EF,这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点E是边BC的中点,因此可以选取AB的中点M,连接EM后尝试着去证△AEM≌EFC就行了,随即小强写出了如下的证明过程:
证明:如图1,取AB的中点M,连接EM.
∵∠AEF=90°
∴∠FEC+∠AEB=90°
又∵∠EAM+∠AEB=90°
∴∠EAM=∠FEC
∵点E,M分别为正方形的边BC和AB的中点
∴AM=EC
又可知△BME是等腰直角三角形
∴∠AME=135°
又∵CF是正方形外角的平分线
∴∠ECF=135°
∴△AEM≌△EFC(ASA)
∴AE=EF
(2)探究2:小强继续探索,如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,发现AE=EF仍然成立,请你证明这一结论.
(3)探究3:小强进一步还想试试,如图3,若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF是否成立呢?若成立请你完成证明过程给小强看,若不成立请你说明理由.
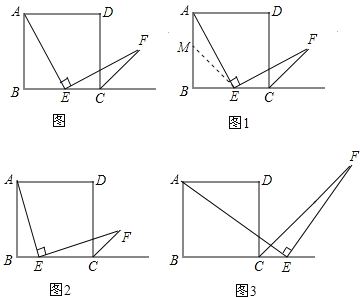
相关试题

