【题目】如图,在△ABC中,AB=AC,∠BAC=56°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为______度.

参考答案:
【答案】112.
【解析】
连接OB、OC,根据角平分线的定义求出∠BAO=28°,利用等腰三角形两底角相等求出∠ABC,根据线段垂直平分线上的点到两端点的距离相等可得OA=OB,再根据等边对等角求出∠OBA,然后求出∠OBC,再根据等腰三角形的性质可得OB=OC,然后求出∠OCE,根据翻折变换的性质可得OE=CE,然后利用等腰三角形两底角相等列式计算即可得解.
如图,连接OB、OC,

∵OA平分∠BAC,∠BAC=56°,
∴∠BAO=![]() ∠BAC=
∠BAC=![]() ×56°=28°,
×56°=28°,
∵AB=AC,∠BAC=56°,
∴∠ABC=![]() (180°∠BAC)=
(180°∠BAC)=![]() ×(180°56°)=62°,
×(180°56°)=62°,
∵OD垂直平分AB,
∴OA=OB,
∴∠OBA=∠BAO=28°,
∴∠OBC=∠ABC∠OBA=62°28°=34°,
由等腰三角形的性质,OB=OC,
∴∠OCE=∠OBC=34°,
∵∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,
∴OE=CE,
∴∠OEC=180°2×34°=112°.
故答案为:112.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙两位同学在长方形的场地ABCD上绕着四周跑步,甲沿着A-D-C-B-A方向循环跑步,同时乙沿着B-C-D-A-B方向循环跑步,AB=30米,BC=50米,若甲速度为2米/秒,乙速度3米/秒.
(1)设经过的时间为t秒,则用含t的代数式表示甲的路程为 米;
(2)当甲、乙两人第一次相遇时,求所经过的时间t为多少秒?
(3)若甲改为沿着A-B-C-D-A的方向循环跑步,而乙仍按原来的方向跑步,两人的速度不变,求经过多少秒,乙追上甲?
(4)在(3)的条件下,当乙第一次追上甲后继续跑步,则最少再经过
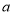 秒乙又追上甲,这时两人所处的位置在点P;直接写出
秒乙又追上甲,这时两人所处的位置在点P;直接写出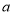 的值,在图中标出点P,不要求书写过程.
的值,在图中标出点P,不要求书写过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=60°,C是BO延长线上一点,OC=12cm,动点P从点C出发沿CB以2cm/s的速度移动,动点Q从点O出发沿OA以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=_____s时,△POQ是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠BAC=60°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作菱形ADEF,使∠DAF=60°,连接CF.
(1)观察猜想:如图1,当点D在线段BC上时,①AB与CF的位置关系为: ;
②BC,CD,CF之间的数量关系为: .
(2)数学思考:如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸:如图3,当点D在线段BC的延长线上时,设AD与CF相交于点G,若已知AB=4,CD=
 AB,求AG的长.
AB,求AG的长.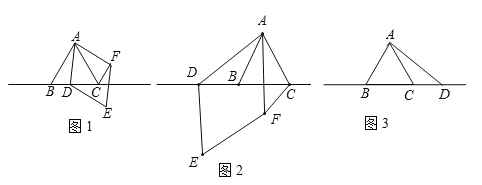
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.

(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)在直线l上找一点P,使PB′+PC的长最短;
(3)若△ACM是以AC为腰的等腰三角形,点M在小正方形的顶点上.这样的点M共有 个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先尺规作图,后进行计算:如图,△ABC中,∠A=105°.

(1)试求作一点P,使得点P到B、C两点的距离相等,并且到∠ABC两边的距离相等(尺规作图,不写作法,保留作图痕迹).
(2)在(1)的条件下,若∠ACP=30°,则∠PBC的度数为 °.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°∠DAB=45°.(1)求∠DAC的度数;(2)请说明:AB=CD.

相关试题

