【题目】如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.

(1)求证:△COD是等边三角形;
(2)当a=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当a为多少度时,△AOD是等腰三角形?
参考答案:
【答案】(1)证明见解析;(2)当α=150°时,△AOD是直角三角形,理由见解析;(3)当α的度数为125°或110°或140°时,△AOD是等腰三角形.
【解析】试题分析:(1)根据旋转的性质可得出![]() ,结合题意即可证得结论;
,结合题意即可证得结论;
(2)结合(1)的结论可作出判断;
(3)找到变化中的不变量,然后利用旋转及全等的性质即可做出解答.
试题解析:(1)证明:∵将△BOC绕点C按顺时针方向旋转![]() 得△ADC,
得△ADC,
∴CO=CD,∠OCD=![]() ,
,
∴△COD是等边三角形,
(2)当![]() 时,△AOD是直角三角形.
时,△AOD是直角三角形.
理由是:∵将△BOC绕点C按顺时针方向旋转60![]() 得△ADC,
得△ADC,
∴△BOC≌△ADC,
![]()
又∵△COD是等边三角形,
∴∠ODC=![]() ,
,
![]()
![]()
![]()
∴△AOD不是等腰直角三角形,即△AOD是直角三角形。
(3)①要使AO=AD,需∠AOD=∠ADO,
![]()
![]()
![]()
②要使OA=OD,需∠OAD=∠ADO.
![]()
![]()
![]()
③要使OD=AD,需∠OAD=∠AOD.
![]()
![]()
![]()
解得![]()
综上所述:当α的度数为![]() 或
或![]() 或
或![]() 时,△AOD是等腰三角形。
时,△AOD是等腰三角形。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B分别是x轴上位于原点左右两侧的点,点P(2,p)在第一象限,直线PA交y轴于点C(0,3),直线PB交y轴于点D,△AOP的面积为12;
(1)求△COP的面积;
(2)求点A的坐标及p的值;
(3)若△BOP与△DOP的面积相等,求直线BD的函数解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△AOB绕着一点旋转到△A′OB′的位置,可以看到点A旋转到点A′,OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段和角.已知∠AOB=30°,∠AOB′=10°,那么点B的对应点是点______;线段OB的对应线段是线段_____;∠A的对应角是______;旋转中心是点_______;旋转的角度是______度.
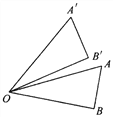
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
, ,求
,求 的值.
的值.解:根据算术平方根的定义,
由
 ,得
,得 ,所以
,所以 ①……第一步
①……第一步根据立方根的定义,
由
 ,得
,得 ②……第二步
②……第二步由①②解得
 ……第三步
……第三步把
 代入
代入 中,得
中,得 ……第四步
……第四步(1)以上解题过程存在错误,请指出错在哪些步骤,并说明错误的原因;
(2)把正确解答过程写出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是( )
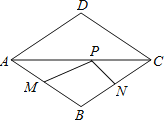
A.
 B. 1 C.
B. 1 C. 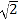 D. 2
D. 2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.
(1)旋转中心是点 ,旋转角度是 度;
(2)若连结EF,则△AEF是 三角形;并证明;
(3)若四边形AECF的面积为25,DE=2,求AE的长.
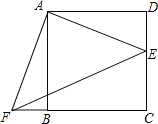
-
科目: 来源: 题型:
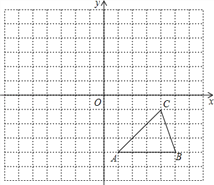
查看答案和解析>>【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
①写出A、B、C的坐标.
②以原点O为对称中心,画出△ABC关于原点O对称的△A1B1C1,并写出A1、B1、C1的坐标.
相关试题

