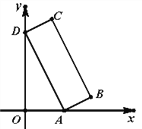
【题目】如图,已知矩形ABCD的顶点A、D分别落在x轴、y轴,OD=2OA=6,AD:AB=3:1.则点B的坐标是_______.
参考答案:
【答案】(5,1)
【解析】过B作BE⊥x轴于E,根据矩形的性质得到∠DAB=90°,根据余角的性质得到∠ADO=∠BAE,根据相似三角形的性质得到AE=![]() OD=2,DE=
OD=2,DE=![]() OA=1,于是得到结论.
OA=1,于是得到结论.
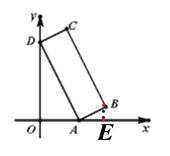
过B作BE⊥x轴于E,
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴∠ADO+∠OAD=∠OAD+∠BAE=90°,
∴∠ADO=∠BAE,
∴△OAD∽△EBA,
∴OD:AE=OA:BE=AD:AB,
∵OD=2OA=6,
∴OA=3.
∵AD:AB=3:1,
∴AE=![]() OD=2,BE=
OD=2,BE=![]() OA=1,
OA=1,
∴OE=3+2=5,
∴B(5,1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN( )

A.AM=CNB.AB=CD C.AM∥CN D.∠M=∠N
-
科目: 来源: 题型:
查看答案和解析>>【题目】为拓宽学生视野,引导学生主动适应社会,促进书本知识和生活经验的深度融合,我市某中学决定组织部分班级去赤壁开展研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.现有甲、乙两种大客车,它们的载客量和租金如表所示.
甲种客车
乙种客车
载客量/(人/辆)
30
42
租金/(元/辆)
300
400
学校计划此次研学旅行活动的租车总费用不超过3100元,为了安全,每辆客车上至少要有2名老师.
(1)参加此次研学旅行活动的老师和学生各有多少人?
(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,可知租用客车总数为 辆;
(3)你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:求代数式
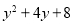 的最小值.
的最小值.解:
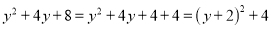
∵
 ≥0,∴
≥0,∴ ≥4
≥4∴
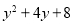 的最小值是4
的最小值是4(1)代数式
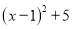 的最小值 ;
的最小值 ;(2)求代数式
 的最小值;
的最小值;(3)某居民小区要在一块一边靠墙(墙长15m)的空地上建一个长方形花园ABCD,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),请问:当x取何值时,花园的面积最大?最大面积是多少.

-
科目: 来源: 题型:
查看答案和解析>>【题目】随着中国传统节日“端午节”的临近,永旺超市决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折.已知打折前,买1盒甲品牌粽子和2盒乙品牌粽子需230元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】初三(1)班要从2男2女共4名同学中选人做晨会的升旗手.
(1)若从这4人中随机选1人,则所选的同学性别为男生的概率是 .
(2)若从这4人中随机选2人,求这2名同学性别相同的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有A、B两种型号的客车,它们的载客量、每天的租金如表所示:
A型号客车
B型号客车
载客量(人/辆)
45
30
租金(元/辆)
600
450
已知某中学计划租用A、B两种型号的客车共10辆,同时送七年级师生到沙家参加社会实践活动,已知该中学租车的总费用不超过5600元.
(1)求最多能租用多少辆A型号客车?
(2)若七年级的师生共有380人,请写出所有可能的租车方案.
相关试题

