【题目】初三(1)班要从2男2女共4名同学中选人做晨会的升旗手.
(1)若从这4人中随机选1人,则所选的同学性别为男生的概率是 .
(2)若从这4人中随机选2人,求这2名同学性别相同的概率.
参考答案:
【答案】(1)![]() ;(2)P(这2名同学性别相同) =
;(2)P(这2名同学性别相同) =![]() .
.
【解析】试题分析:(1)用男生人数2除以总人数4即可得出答案;
(2)根据题意先画出树状图,得出所有情况数,再根据概率公式即可得出答案.
解:(1)![]() ;
;
(2)从4人中随机选2人,所有可能出现的结果有:(男1,男2)、(男1,女1)、(男1,女2)、(男2,男1)、(男2,女1)、(男2,女2)、(女1,男1)、(女1,男2)、(女1,女2)、(女2,男1)、(女2,男2)、(女2,女1),共有12种,它们出现的可能性相同,
所以满足“这2名同学性别相同”(记为事件A)的结果有种,所以P(A)=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:求代数式
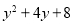 的最小值.
的最小值.解:
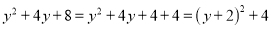
∵
 ≥0,∴
≥0,∴ ≥4
≥4∴
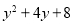 的最小值是4
的最小值是4(1)代数式
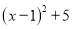 的最小值 ;
的最小值 ;(2)求代数式
 的最小值;
的最小值;(3)某居民小区要在一块一边靠墙(墙长15m)的空地上建一个长方形花园ABCD,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),请问:当x取何值时,花园的面积最大?最大面积是多少.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD的顶点A、D分别落在x轴、y轴,OD=2OA=6,AD:AB=3:1.则点B的坐标是_______.
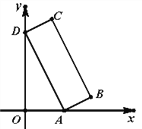
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着中国传统节日“端午节”的临近,永旺超市决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折.已知打折前,买1盒甲品牌粽子和2盒乙品牌粽子需230元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有A、B两种型号的客车,它们的载客量、每天的租金如表所示:
A型号客车
B型号客车
载客量(人/辆)
45
30
租金(元/辆)
600
450
已知某中学计划租用A、B两种型号的客车共10辆,同时送七年级师生到沙家参加社会实践活动,已知该中学租车的总费用不超过5600元.
(1)求最多能租用多少辆A型号客车?
(2)若七年级的师生共有380人,请写出所有可能的租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
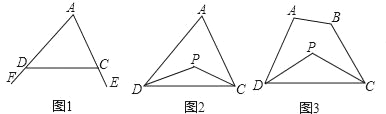
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:

(1)请将下表补充完整:

(2)请从下列三个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看, 的成绩好些;
②从平均数和中位数相结合看, 的成绩好些;
③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.
相关试题

