【题目】某地区住宅用电之电费计算规则如下:每月每户不超过50度时,每度以4元收费;超过50度的部分,每度以5元收费,并规定用电按整数度计算(小数部份无条件舍去).
(1)下表给出了今年3月份A,B两用户的部分用电数据,请将表格数据补充完整,
电量(度) | 电费(元) | |
A | 240 | |
B | ||
合计 | 90 |
(2)若假定某月份C用户比D用户多缴电费38元,求C用户该月可能缴的电费为多少?
参考答案:
【答案】
(1)58;32;128;368
(2)解:设3月份C用户用电x度,D用户用电y度.
∵38不能被4和5整除,
∴x>50,y≤50,
∴200+5(x﹣50)﹣4y=38
∴5x﹣4y=88,
∴ ![]() .
.
∵ ![]() ,
,
∴50<x≤57.6.
又∵x是4的倍数,
∴x=52,56 C用户可能缴的缴电费为210元或230元.
【解析】解:(1)设A用户用电量为x度,则 4×50+5(x﹣50)=240,
解得x=58;
B用户的用电量:90﹣58=32(度).
B用户的电费:32×4=128(元)
A、B用户的电费:240+128=368(元),
故答案是:
电量(度) | 电费(元) | |
A | 58 | 240 |
B | 32 | 128 |
合计 | 90 | 368 |
(1)根据收费标准和电费=相应段的收费标准×用电量进行计算;(2)设3月份C用户用电x度,D用户用电y度.结合(1)中求得的相关数据得到:x>50,y≤50,200+5(x﹣50)﹣4y=38,求x、y的整数解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线m,n的夹角为35°,相交于点O.
(1)作出△ABC关于直线m的对称△DEF;
(2)作出△DEF关于直线n的对称△PQR;
(3)△PQR还可以由△ABC经过一次怎样的变换得到.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是( )
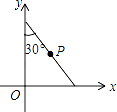
A.(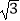 ,1)
,1)
B.(1,﹣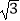 )
)
C.(2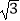 ,﹣2)
,﹣2)
D.(2,﹣2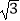 )
) -
科目: 来源: 题型:
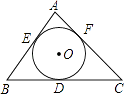
查看答案和解析>>【题目】如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠A=80°,点P为⊙O上任意一点(不与E、F重合),则∠EPF= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年5月27日,太原与大同之间开通了“点对点”的云冈号旅游列车(中间不停车),该列车为空调车,由6节硬座车厢、1节软卧车厢、1节硬卧车厢组成.行驶的路程约300km,该旅游列车从太原站出发,以平均速度110km/h开往大同.用x(h)表示列车行驶的时间,y(km)表示列车距大同的距离.
(1)写出y与x之间的函数关系式;
(2)当该旅游列车距大同就还有80km时,求行驶了多长时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.
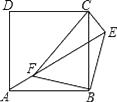
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直角坐标系中有一矩形OABC,其中O是坐标原点,点A,C分别在x轴和y轴上,点B的坐标为(3,4),直线y=
 x交AB于点D,点P是直线y=
x交AB于点D,点P是直线y=  x位于第一象限上的一点,连接PA,以PA为半径作⊙P,
x位于第一象限上的一点,连接PA,以PA为半径作⊙P, 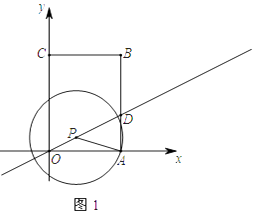
(1)连接AC,当点P落在AC上时,求PA的长;
(2)当⊙P经过点O时,求证:△PAD是等腰三角形;
(3)设点P的横坐标为m, ①在点P移动的过程中,当⊙P与矩形OABC某一边的交点恰为该边的中点时,求所有满足要求的m值;
②如图2,记⊙P与直线y= x的两个交点分别为E,F(点E在点P左下方),当DE,DF满足
x的两个交点分别为E,F(点E在点P左下方),当DE,DF满足  <
< 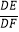 <3时,求m的取值范围.(请直接写出答案)
<3时,求m的取值范围.(请直接写出答案)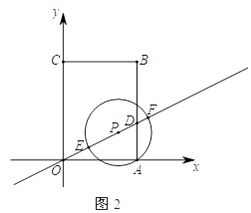
相关试题

