【题目】某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).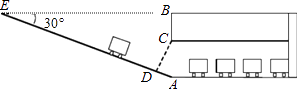
参考答案:
【答案】解:由题意得,AB⊥EB,CD⊥AE,

∴∠CDA=∠EBA=90°,
∵∠E=30°,
∴AB= ![]() AE=8米,
AE=8米,
∵BC=1.2米,
∴AC=AB﹣BC=6.8米,
∵∠DCA=90°﹣∠A=30°,
∴CD=AC×cos∠DCA=6.8× ![]() ≈5.9米.
≈5.9米.
答:该校地下停车场的高度AC为6.8米,限高CD约为5.9米.
【解析】本题主要考查了解直角三角形的应用-仰角俯角问题,先根据题意和正弦的定义求出AB的长,根据余弦的定义求出CD的长即可.
【考点精析】关于本题考查的关于仰角俯角问题,需要了解仰角:视线在水平线上方的角;俯角:视线在水平线下方的角才能得出正确答案.
-
科目: 来源: 题型:
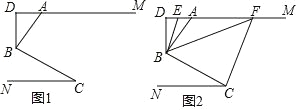
查看答案和解析>>【题目】如图 1,AM∥CN,点 B 为平面内一点,AB⊥BC 于 B,过 B 作 BD⊥ AM.
(1)求证:∠ABD=∠C;
(2)如图 2,在(1)问的条件下,分别作∠ABD、∠DBC 的平分线交 DM 于 E、F,若∠BFC=1.5∠ABF,∠FCB=2.5∠BCN,
①求证:∠ABF=∠AFB;
②求∠CBE 的度数.
-
科目: 来源: 题型:
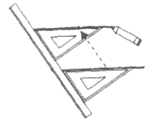
查看答案和解析>>【题目】如图,利用直尺和三角尺过直线外一点画已知直线的平行线,这种画法依据的是____________。
-
科目: 来源: 题型:
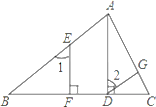
查看答案和解析>>【题目】完成下列证明:如图,已知AD⊥BC,EF⊥BC,∠1=∠2.
求证: DG∥BA.
证明:∵AD⊥BC,EF⊥BC ( 已知 )
∴∠EFB=90°,∠ADB=90°(_______________________ )
∴∠EFB=∠ADB ( 等量代换 )
∴EF∥AD ( _________________________________ )
∴∠1=∠BAD (________________________________________)
又∵∠1=∠2 ( 已知)
∴ (等量代换)
∴DG∥BA. (__________________________________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.

(1)求证:DE是⊙O的切线;
(2)若AE=6,CE=2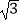 ,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π) -
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)实施新课程改革后,学生的自主学习、合作交流能力有很大提高,张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期三个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)本次调查中,张老师一共调查了 名同学,其中C类女生有 名,D类男生有 名;
(2)将上面的条形统计图补充完整;
(3)为了共同进步,张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调,如表是近两周的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
5台
18000元
第二周
4台
10台
31000元
(进价、售价均保持不变,利润=销售总收入进货成本)
(1)求A、B两种型号的空调的销售单价;
(2)若超市准备用不多于54000元的金额再采购这两种型号的空调共30台,求A种型号的空调最多能采购多少台?
相关试题

