【题目】如图,![]() 为圆
为圆![]() 的直径,
的直径,![]() 为圆
为圆![]() 上一点,
上一点,![]() 为
为![]() 延长线一点,且
延长线一点,且![]() ,
,![]() 于点
于点![]() .
.
(1)求证:直线![]() 为圆
为圆![]() 的切线;
的切线;
(2)设![]() 与圆
与圆![]() 交于点
交于点![]() ,
,![]() 的延长线与
的延长线与![]() 交于点
交于点![]() ,
,
①求证:![]()
②若![]() ,
,![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)见解析;(2)①见解析;②![]()
【解析】
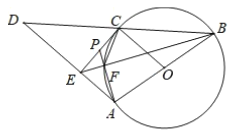
(1)说明OC是△BDA的中位线,利用中位线的性质,得到∠OCE=∠CED=90°,从而得到CE是圆O的切线.
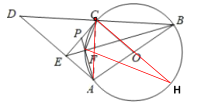
(2)①过点![]() 作直径
作直径![]() ,连接
,连接![]() ,
,![]() ,运用已知条件证明
,运用已知条件证明![]() ,即可得到
,即可得到![]() ,即
,即![]() .
.
②利用直径上的圆周角,得到△PEF是直角三角形,利用角相等,可得到△PEF∽△PEA、△PCF∽△PAC,从而得到PC=PE=5.然后求出sin∠PEF的值
(1)证明:∵![]() 于点
于点![]() ∴
∴![]() ,
,
∵![]() ,∴
,∴![]() 是
是![]() 的中点,又∵
的中点,又∵![]() 是
是![]() 的中点,
的中点,
∴![]() 是
是![]() 的中位线,
的中位线,
∴![]() ,∴
,∴![]()
∴![]() ,又∵点
,又∵点![]() 在圆上,
在圆上,
∴![]() 是圆
是圆![]() 的切线.
的切线.
(2)①证明:过点![]() 作直径
作直径![]() ,连接
,连接![]() ,
,![]() ,
,
∵![]() 是直径,∴
是直径,∴![]() ∴
∴![]()
∵![]() 是圆
是圆![]() 的切线,∴
的切线,∴![]() ,
,
∴![]() ∴
∴![]()
∵![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]()
∴![]() ∴
∴![]() .
.
②∵直径![]() ,∴
,∴![]() 即
即![]()
∵![]() ∴
∴![]()
∵![]() ∴
∴![]()
∴![]() ∴
∴![]()
∵![]() ∴
∴![]()
在![]() 中
中![]() .
.

-
科目: 来源: 题型:
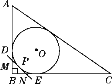
查看答案和解析>>【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN,与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )
A. r B.
 r C. 2r D.
r C. 2r D.  r
r -
科目: 来源: 题型:
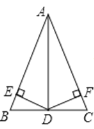
查看答案和解析>>【题目】如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,BE=CF.
求证:(1)△BDE≌△CDF;
(2)AD是△ABC的角平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角三角形ABC中,∠ABC=90°,D为AC边上的中点,过D点作DE⊥DF,交AB于点E,交BC于点F,若AE=8,FC=6.
(1)求EF的长.
(2)求四边形BEDF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线的顶点
 ,且经过点
,且经过点 ,与
,与 轴分别交于
轴分别交于 两点.
两点.
(1)求直线
 和该抛物线的解析式;
和该抛物线的解析式;(2)如图1,点
 是抛物线上的一个动点,且在直线
是抛物线上的一个动点,且在直线 的上方,过点
的上方,过点 作
作 轴的平行线与直线
轴的平行线与直线 交于点
交于点 ,求
,求 的最大值;
的最大值;(3)如图2,
 轴交
轴交 轴于点
轴于点 ,点
,点 是抛物线上
是抛物线上 、
、 之间的一个动点,直线
之间的一个动点,直线 、
、 与
与 分别交于
分别交于 、
、 ,当点
,当点 运动时,求
运动时,求 的值.
的值. -
科目: 来源: 题型:
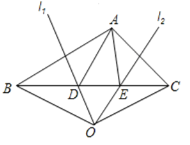
查看答案和解析>>【题目】如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连结0B,OC.若△ADE的周长为12cm,△OBC的周长为32cm.
(1)求线段BC的长;
(2)连结OA,求线段OA的长;
(3)若∠BAC=n°(n>90),直接写出∠DAE的度数 °.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正六边形ABCDEF是边长为2 cm的螺母,点P是FA延长线上的点,在A,P之间拉一条长为12 cm的无伸缩性细线,一端固定在点A,握住另一端点P拉直细线,把它全部紧紧缠绕在螺母上(缠绕时螺母不动),则点P运动的路径长为( )
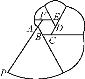
A. 13π cm B. 14π cm C. 15π cm D. 16π cm
相关试题

