【题目】阅读下面材料:
在数轴上2与﹣1所对的两点之间的距离:|2﹣(﹣1)|=3;
在数轴上﹣2与3所对的两点之间的距离:|﹣2﹣3|=5;
在数轴上﹣3与﹣1所对的两点之间的距离:|(﹣1)﹣(﹣3)|=2
归纳:在数轴上点A、B分别表示数a、b,则A、B两点之间的距离AB=|a﹣b|或|b﹣a|

回答下列问题:
(1) 数轴上表示数x和1的两点之间的距离表示为 ;数轴上表示数x和 的两点之间的距离表示为|x+2|;
(2)请你在草稿纸上画出数轴,当表示数x的点在﹣2与3之间移动时,|x﹣3|+|x+2|的值总是一个固定的值为: .
(3)继续请你在草稿纸上画出数轴,探究当x=_______时,|x-3|+|x+2|=7.
参考答案:
【答案】(1)|x-1|,-2;(2)5;(3)-3或4.
【解析】
(1)根据题意找出数轴上任意点间的距离的计算公式,然后进行计算即可;
(2)先化简绝对值,然后合并同类项即可;
(3)分为x>3和x<-2两种情况讨论.
(1)数轴上表示x和1的两点之间的距离=|x-1|;
数轴上表示数x和2的两点之间的距离表示为|x+2|;
(2)∵表示数x的点在﹣2与3之间移动,
∴2x3
当2x3时,|x-3|+|x+2|=3x + x+2=5;
(3)由(2)可知当2x3时,|x﹣3|+|x+2|的值总是一个固定的值5,不等于7;
所以可分两种情况:
当x>3时,x3+x+2=7,
解得:x=4;
当x<2时,3xx2=7.
解得x=3.
∴x=3或x=4.
故答案为:(1)|x-1|,-2;(2)5;(3)-3或4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.

求证:(1)△AFD≌△CEB.(2)四边形ABCD是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点A表示的数a、点B表示数b,a、b满足|a﹣30|+(b+6)2=0.点O是数轴原点.

(1)点A表示的数为 ,点B表示的数为 ,线段AB的长为 .
(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在数轴上找一点C,使AC=2BC,则点C在数轴上表示的数为 .
(3)现有动点P、Q都从B点出发,点P以每秒1个单位长度的速度向终点A移动;当点P移动到O点时,点Q才从B点出发,并以每秒3个单位长度的速度向右移动,且当点P到达A点时,点Q就停止移动,设点P移动的时间为t秒,问:当t为多少时,P、Q两点相距4个单位长度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知不在同一条直线上的三点A,B,C.
(1)按下列要求作图(用尺规作图,不要求写做法,但要保留作图痕迹,并书写结论)
①分别作射线BA,线段AC;
②在线段BA的延长线上作AD=AC.
(2)若∠CAD比∠CAB大100°,则∠CAB的度数为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ADB=∠ADC,则不一定能使△ABD≌△ACD的条件是( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BAD=∠CAD
-
科目: 来源: 题型:
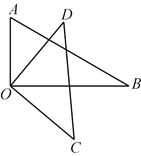
查看答案和解析>>【题目】如图,将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
(1)判断大小关系:∠AOD______∠BOC(填>、=、<等)
(2)若 ∠BOD=35°,则∠AOC= ;若∠AOC=135°,则∠BOD= ;
(3)猜想 ∠AOC与∠BOD的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CA⊥AB,垂足为点A,AB=8,AC=4,射线BM⊥AB,垂足为点B,一动点E从A点出发以2厘米/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E离开点A后,运动______ 秒时,△DEB与△BCA全等.

相关试题

