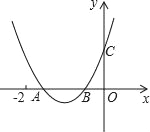
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,且OB=OC,下列结论:①b>1且b≠2;②b2﹣4ac<4a2;③a>![]() ;其中正确的个数为( )
;其中正确的个数为( )
A. 0 B. 1 C. 2 D. 3
参考答案:
【答案】D
【解析】①∵OB=OC,
∴C(0,c),B(﹣c,0)
把B(﹣c,0)代入y=ax2+bx+c得0=ac2﹣bc+c,即0=ac2+c(1﹣b),
∵a>0,
∴1﹣b<0,即b>1,
如果b=2,由0=ac2﹣bc+c,可得ac=1,此是△=b2﹣4ac=0,故b>1且b≠2正确,
②∵a>0,b>0,c>0,设C(0,c),B(﹣c,0)
∵AB=|x1﹣x2|<2,
∴(x1+x2)2﹣4x1x2<4,
∴(﹣![]() )2﹣4×
)2﹣4×![]() <4,即
<4,即![]() ﹣
﹣![]() <4,
<4,
∴b2﹣4ac<4a2;故本项正确.
③把B(﹣c,0)代入y=ax2+bx+c可得ac+1=b,
代入y=ax2+bx+c得y=ax2+(ac+1)x+c=ax2+acx+x+c=ax2+x+acx+c=x(ax+1)+c(ax+1)=(x+c)(ax+1),
解得x1=﹣c,x2=﹣![]() ,
,
由图可得x1,x2>﹣2,
即﹣![]() >﹣2,
>﹣2,
∵a>0,
∴![]() <2,
<2,
∴a>![]() ;正确.
;正确.
所以正确的个数是3个.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(-4,0).
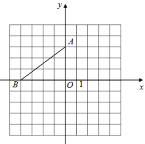
(1)画出△AOB绕点A逆时针旋转90°后得到的图形△A1O1B1;并写出点B1的坐标 ;
(2)画出△AOB关于点P(0,-1)的中心对称图形△A2O2B2,并写出点B2的坐标 ;
(3)若点Q为x轴上的一点,当B1Q+B2 Q的和最小时,直接写出点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把2张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.阴影部分刚好能分割成两张形状大小不同的小长方形卡片(如图③),则分割后的两个阴影长方形的周长和是( )

A. 4mB. 2(m+n)C. 4nD. 4(m﹣n)
-
科目: 来源: 题型:
查看答案和解析>>【题目】邮递员骑车从邮局出发,先向西骑行 2 km 到达 A 村,继续向西骑行 3 km 到达 B 村, 然后向东骑行 9 km 到达 C 村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用 1 cm 表示 1 km 画数轴,并在该数轴上表示 A,B,C 三个村庄的位置;
(2)C 村离 A 村有多远?
(3)邮递员一共骑行了多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】[新定义]:
 为数轴上三点,若点
为数轴上三点,若点 到点
到点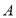 的距离是点
的距离是点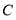 到点
到点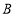 的距离的3倍,我们就称点
的距离的3倍,我们就称点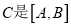 的幸运点.
的幸运点.[特例感知]
(1)如图1,点
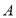 表示的数为-1,点
表示的数为-1,点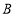 表示的数为3.表示2的点
表示的数为3.表示2的点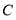 到点
到点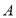 的距离是3,到点
的距离是3,到点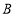 的距离是1,那么点
的距离是1,那么点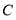 是
是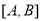 的幸运点,
的幸运点,①
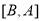 的幸运点表示的数是________;
的幸运点表示的数是________;A.-1 B.0 C.1 D.2
②试说明
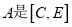 的幸运点.
的幸运点.(2)如图2,
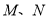 为数轴上两点,点
为数轴上两点,点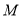 所表示的数为-2,点
所表示的数为-2,点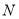 所表示的数为4,
所表示的数为4,则
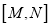 的幸运点表示的数为________.
的幸运点表示的数为________.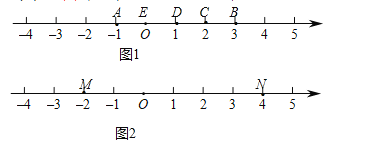
[拓展应用]
(3)如图3,
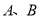 为数轴上两点,点
为数轴上两点,点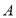 所表示的数为-20,点
所表示的数为-20,点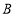 所表示的数为40.有一只电子蚂蚁
所表示的数为40.有一只电子蚂蚁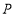 从点
从点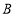 出发,以5个单位每秒的速度向左运动,到达点
出发,以5个单位每秒的速度向左运动,到达点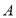 停止.当t为何值时,
停止.当t为何值时,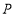 、
、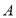 和
和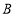 三个点中恰好有一个点为其余两点的幸运点?
三个点中恰好有一个点为其余两点的幸运点?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=﹣x+4的图象与反比例函数y=
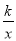 (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】
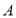 、
、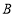 两地相距
两地相距 ,甲、乙两车分别从
,甲、乙两车分别从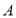 、
、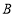 两地同时出发,相向而行.已知甲车速度为
两地同时出发,相向而行.已知甲车速度为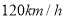 ,乙车速度为
,乙车速度为 ,经过
,经过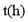 后两车相距
后两车相距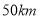 ,则
,则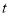 的值是( )
的值是( )A.2B.10C.2或10D.2或2.5
相关试题

