【题目】如图,一次函数y=﹣x+4的图象与反比例函数y=![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.

参考答案:
【答案】(1)反比例函数的表达式y=![]() ,点B的坐标为(3,1).(2)
,点B的坐标为(3,1).(2)![]() .
.
【解析】试题分析:(1)由点A在一次函数图象上,结合一次函数解析式可求出点A的坐标,再由点A的坐标利用待定系数法即可求出反比例函数解析式,联立两函数解析式成方程组,解方程组即可求出点B坐标;
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,连接PB.由点B、D的对称性结合点B的坐标找出点D的坐标,设直线AD的解析式为y=mx+n,结合点A、D的坐标利用待定系数法求出直线AD的解析式,令直线AD的解析式中y=0求出点P的坐标,再通过分割图形结合三角形的面积公式即可得出结论.
试题解析:(1)把点A(1,a)代入一次函数y=-x+4,
得:a=-1+4,解得:a=3,
∴点A的坐标为(1,3).
把点A(1,3)代入反比例函数y=![]() ,
,
得:3=k,
∴反比例函数的表达式y=![]() ,
,
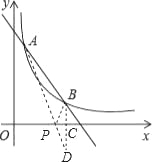
联立两个函数关系式成方程组得: 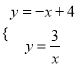 ,
,
解得: ![]() ,或
,或![]() ,
,
∴点B的坐标为(3,1).
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,此时PA+PB的值最小,连接PB,如图所示.
∵点B、D关于x轴对称,点B的坐标为(3,1),
∴点D的坐标为(3,- 1).
设直线AD的解析式为y=mx+n,
把A,D两点代入得: ![]() ,
,
解得: ![]() ,
,
∴直线AD的解析式为y=-2x+5.
令y=-2x+5中y=0,则-2x+5=0,
解得:x=![]() ,
,
∴点P的坐标为(![]() ,0).
,0).
S△PAB=S△ABD-S△PBD=![]() BD(xB-xA)-
BD(xB-xA)-![]() BD(xB-xP)
BD(xB-xP)
=![]() ×[1-(-1)]×(3-1)-
×[1-(-1)]×(3-1)-![]() ×[1-(-1)]×(3-
×[1-(-1)]×(3-![]() )
)
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】邮递员骑车从邮局出发,先向西骑行 2 km 到达 A 村,继续向西骑行 3 km 到达 B 村, 然后向东骑行 9 km 到达 C 村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用 1 cm 表示 1 km 画数轴,并在该数轴上表示 A,B,C 三个村庄的位置;
(2)C 村离 A 村有多远?
(3)邮递员一共骑行了多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,且OB=OC,下列结论:①b>1且b≠2;②b2﹣4ac<4a2;③a>
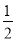 ;其中正确的个数为( )
;其中正确的个数为( )
A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】[新定义]:
 为数轴上三点,若点
为数轴上三点,若点 到点
到点 的距离是点
的距离是点 到点
到点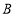 的距离的3倍,我们就称点
的距离的3倍,我们就称点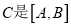 的幸运点.
的幸运点.[特例感知]
(1)如图1,点
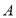 表示的数为-1,点
表示的数为-1,点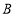 表示的数为3.表示2的点
表示的数为3.表示2的点 到点
到点 的距离是3,到点
的距离是3,到点 的距离是1,那么点
的距离是1,那么点 是
是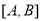 的幸运点,
的幸运点,①
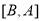 的幸运点表示的数是________;
的幸运点表示的数是________;A.-1 B.0 C.1 D.2
②试说明
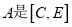 的幸运点.
的幸运点.(2)如图2,
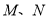 为数轴上两点,点
为数轴上两点,点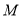 所表示的数为-2,点
所表示的数为-2,点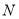 所表示的数为4,
所表示的数为4,则
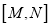 的幸运点表示的数为________.
的幸运点表示的数为________.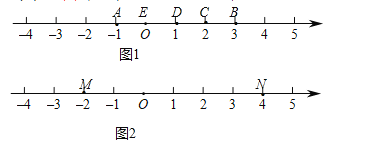
[拓展应用]
(3)如图3,
 为数轴上两点,点
为数轴上两点,点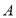 所表示的数为-20,点
所表示的数为-20,点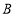 所表示的数为40.有一只电子蚂蚁
所表示的数为40.有一只电子蚂蚁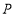 从点
从点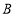 出发,以5个单位每秒的速度向左运动,到达点
出发,以5个单位每秒的速度向左运动,到达点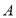 停止.当t为何值时,
停止.当t为何值时,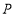 、
、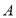 和
和 三个点中恰好有一个点为其余两点的幸运点?
三个点中恰好有一个点为其余两点的幸运点?
-
科目: 来源: 题型:
查看答案和解析>>【题目】
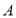 、
、 两地相距
两地相距 ,甲、乙两车分别从
,甲、乙两车分别从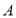 、
、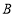 两地同时出发,相向而行.已知甲车速度为
两地同时出发,相向而行.已知甲车速度为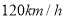 ,乙车速度为
,乙车速度为 ,经过
,经过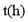 后两车相距
后两车相距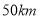 ,则
,则 的值是( )
的值是( )A.2B.10C.2或10D.2或2.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商家今年3月份两次同时购进了甲、乙两种不同单价的糖果,第一次购买甲种糖果的数量比乙种糖果的数量多50%,第二次购买甲种糖果的数量比第一次购买甲种糖果的数量少60%,结果第二次购买糖果的总数量虽然比第一次购买糖果的总数量多20%,但第二次购买甲乙糖果的总费用却比第一次购买甲乙糖果的总费用费少10%.(甲,乙两种糖果的单价不变),则乙种糖果的单价是甲种糖果单价的_____%.
-
科目: 来源: 题型:
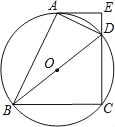
查看答案和解析>>【题目】如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE.
(1)求证:AE⊥CD;
(2)已知AE=4cm,CD=6cm,求⊙O的半径.
相关试题

