【题目】已知,BC∥OA,∠B=∠A=108°,试解答下列问题:
(1)如图1所示,则∠O= °,并判断OB与AC平行吗?为什么?
(2)如图2,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.则∠EOC的度数等于 °;
(3)在第(2)题的条件下,若平行移动AC,如图3.
①求∠OCB:∠OFB的值;
②当∠OEB=∠OCA时,求∠OCA的度数(直接写出答案,不必写出解答过程).

参考答案:
【答案】(1)72,OB∥AC,见解析;(2)40;(3)①∠OCB:∠OFB=1:2;②∠OCA=54°
【解析】
(1)首先根据平行线的性质可得∠B+∠O=180![]() ,再根据∠A=∠B可得∠A+∠O=180
,再根据∠A=∠B可得∠A+∠O=180![]() ,进而得到OB∥AC;
,进而得到OB∥AC;
(2)根据角平分线的性质可得∠EOF=![]() ∠BOF,∠FOC=
∠BOF,∠FOC=![]() ∠FOA,进而得到∠EOC=
∠FOA,进而得到∠EOC=![]() (∠BOF+∠FOA)=
(∠BOF+∠FOA)=![]() ∠BOA=40
∠BOA=40![]() ;
;
(3)①由BC∥OA可得∠FCO=∠COA,进而得到∠FOC=∠FCO,故∠OFB=∠FOC+∠FCO=2∠OCB,进而得到∠OCB:∠OFB=1:2;
②由(1)知:OB∥AC,BC∥OA,得到∠OCA=∠BOC,∠OEB=∠EOA,根据(1)、(2)的结果求得.
解:(1)∵BC∥OA,∠B=108![]()
∴∠O=180![]() -108
-108![]() =72
=72![]() ,
,
∵BC∥OA,
∴∠B+∠O=180![]() ,
,
∵∠A=∠B
∴∠A+∠O=180![]() ,
,
∴OB∥AC
故答案为:72![]() ;
;
(2)∵∠A=∠B=108![]() ,由(1)得∠BOA=180
,由(1)得∠BOA=180![]() ﹣∠B=72
﹣∠B=72![]() ,
,
∵∠FOC=∠AOC,并且OE平分∠BOF,
∴∠EOF=![]() ∠BOF,∠FOC=
∠BOF,∠FOC=![]() ∠FOA,
∠FOA,
∴∠EOC=∠EOF+∠FOC=![]() (∠BOF+∠FOA)=
(∠BOF+∠FOA)=![]() ∠BOA=36
∠BOA=36![]()
故答案为:36![]() ;
;
(3)①∵BC∥OA,
∴∠FCO=∠COA,
又∵∠FOC=∠AOC,
∴∠FOC=∠FCO,
∴∠OFB=∠FOC+∠FCO=2∠OCB,
∴∠OCB:∠OFB=1:2;
②由(1)知:OB∥AC,∴∠OCA=∠BOC,
由(2)可以设:∠BOE=∠EOF=α,∠FOC=∠COA=β,
∴∠OCA=∠BOC=2α+β
由(1)知:BC∥OA,
∴∠OEB=∠EOA=α+β+β=α+2β
∵∠OEB=∠OCA
∴2α+β=α+2β
∴α=β
∵∠AOB=72![]() ,
,
∴α=β=18![]()
∴∠OCA=2α+β=36![]() +18
+18![]() =54
=54![]() .
.
-
科目: 来源: 题型:
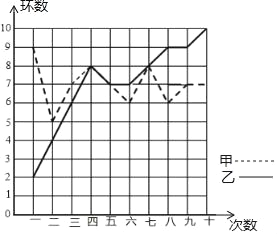
查看答案和解析>>【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:
(1)请将下表补充完整:(参考公式:方差S2=
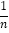 [(x1﹣
[(x1﹣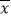 )2+(x2﹣
)2+(x2﹣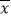 )2+…+(xn﹣
)2+…+(xn﹣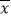 )2])
)2])平均数
方差
中位数
甲
7
7
乙
5.4
(2)请从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看, 的成绩好些;
②从平均数和中位数相结合看, 的成绩好些;
③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.
-
科目: 来源: 题型:
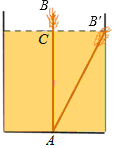
查看答案和解析>>【题目】如图,有一个水池,其底面是边长为16尺的正方形,一根芦苇AB生长在它的正中央,高出水面部分BC的长为2尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B′,则这根芦苇AB的长是( )
A. 15尺B. 16尺C. 17尺D. 18尺
-
科目: 来源: 题型:
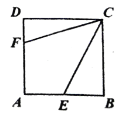
查看答案和解析>>【题目】如图,正方形
 的边长为12,点
的边长为12,点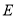 、
、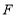 分别在
分别在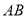 、
、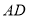 上,若
上,若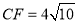 ,且
,且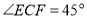 ,则
,则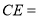 ______.
______.
-
科目: 来源: 题型:
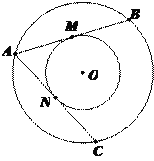
查看答案和解析>>【题目】如图,大圆的弦AB、AC分别切小圆于点M、N.
(1)求证:AB=AC;
(2)若AB=8,求圆环的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
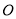 是直线
是直线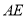 上一点,
上一点,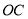 平分
平分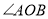 ,
,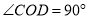 .则图中互余的角、互补的角各有( )对
.则图中互余的角、互补的角各有( )对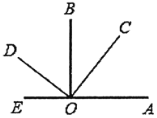
A.4,7B.4,4C.4,5D.3,3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:O是直线AB上的一点,
 是直角,OE平分
是直角,OE平分 .
.(1)如图1.若
 .求
.求 的度数;
的度数;(2)在图1中,
 ,直接写出
,直接写出 的度数(用含a的代数式表示);
的度数(用含a的代数式表示);(3)将图1中的
 绕顶点O顺时针旋转至图2的位置,探究
绕顶点O顺时针旋转至图2的位置,探究 和
和 的度数之间的关系.写出你的结论,并说明理由.
的度数之间的关系.写出你的结论,并说明理由.
相关试题

