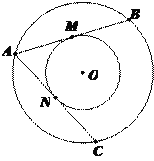
【题目】如图,大圆的弦AB、AC分别切小圆于点M、N.
(1)求证:AB=AC;
(2)若AB=8,求圆环的面积.
参考答案:
【答案】(1)证明见解析;(2)S圆环=16π
【解析】试题分析:(1)连结OM、ON、OA由切线长定理可得AM=AN,由垂径定理可得AM=BM,AN=NC,从而可得AB=AC.
(2)由垂径定理可得AM=BM=4,由勾股定理得OA2-OM2=AM 2=16,代入圆环的面积公式求解即可.
(1)证明:连结OM、ON、OA
∵AB、AC分别切小圆于点M、N.
∴AM=AN,OM⊥AB,ON⊥AC,
∴AM=BM,AN=NC,
∴AB=AC
(2)解:∵弦AB切与小圆⊙O相切于点M
∴OM⊥AB
∴AM=BM=4
∴在Rt△AOM中,OA2-OM2=AM 2=16
∴S圆环=πOA2-πOM2=πAM 2=16π
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一个水池,其底面是边长为16尺的正方形,一根芦苇AB生长在它的正中央,高出水面部分BC的长为2尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B′,则这根芦苇AB的长是( )
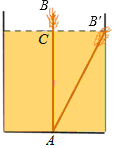
A. 15尺B. 16尺C. 17尺D. 18尺
-
科目: 来源: 题型:
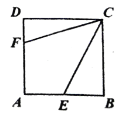
查看答案和解析>>【题目】如图,正方形
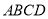 的边长为12,点
的边长为12,点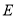 、
、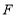 分别在
分别在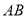 、
、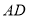 上,若
上,若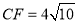 ,且
,且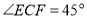 ,则
,则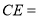 ______.
______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,BC∥OA,∠B=∠A=108°,试解答下列问题:
(1)如图1所示,则∠O= °,并判断OB与AC平行吗?为什么?
(2)如图2,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.则∠EOC的度数等于 °;
(3)在第(2)题的条件下,若平行移动AC,如图3.
①求∠OCB:∠OFB的值;
②当∠OEB=∠OCA时,求∠OCA的度数(直接写出答案,不必写出解答过程).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
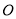 是直线
是直线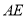 上一点,
上一点,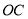 平分
平分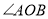 ,
,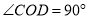 .则图中互余的角、互补的角各有( )对
.则图中互余的角、互补的角各有( )对
A.4,7B.4,4C.4,5D.3,3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:O是直线AB上的一点,
 是直角,OE平分
是直角,OE平分 .
.(1)如图1.若
 .求
.求 的度数;
的度数;(2)在图1中,
 ,直接写出
,直接写出 的度数(用含a的代数式表示);
的度数(用含a的代数式表示);(3)将图1中的
 绕顶点O顺时针旋转至图2的位置,探究
绕顶点O顺时针旋转至图2的位置,探究 和
和 的度数之间的关系.写出你的结论,并说明理由.
的度数之间的关系.写出你的结论,并说明理由.
-
科目: 来源: 题型:
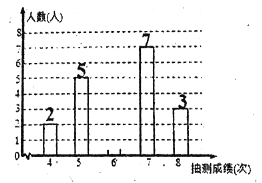
查看答案和解析>>【题目】为了解某校八年级男生的体能情况,体育老师从中随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成两个不完整的统计图,请结合图中信息回答下列问题:
(1)本次抽测的男生有 人,请将条形图补充完成,本次抽测成绩的中位数是 次;
(2)若规定引体向上6次及其以上为体能达标,则该校500名八年级男生中估计有多少人体能达标?

相关试题

