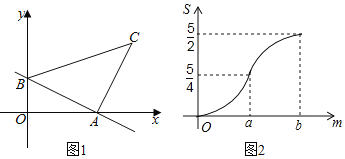
【题目】如图1,直线AB与x轴、y轴分别相交于点A、B,将线段AB绕点A顺时针旋转90°,得到AC,连接BC,将△ABC沿射线BA平移,当点C到达x轴时运动停止.设平移距离为m,平移后的图形在x轴下方部分的面积为S,S关于m的函数图象如图2所示(其中0<m≤a,a<m≤b时,函数的解析式不同).
(1)填空:△ABC的面积为 ;
(2)求直线AB的解析式;
(3)求S关于m的解析式,并写出m的取值范围.
参考答案:
【答案】(1)![]() ;(2)直线AB的解析式为y=﹣
;(2)直线AB的解析式为y=﹣![]() x+1;(3)S=
x+1;(3)S=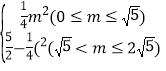 .
.
【解析】(1)由图2结合平移即可得出结论;
(2)判断出△AOB≌△CEA,得出AE=OB,CE=OA,再由图2知,点C的纵坐标是点B纵坐标的2倍,即可利用三角形ABC的面积求出OB,OA,即可得出结论;
(3)分两种情况,利用三角形的面积公式或三角形的面积差即可得出结论.
(1)结合△ABC的移动和图2知,点B移动到点A处,就是图2中,m=a时,S=S△A'B'D=![]() ,点C移动到x轴上时,即:m=b时,S=S△A'B'C'=S△ABC=
,点C移动到x轴上时,即:m=b时,S=S△A'B'C'=S△ABC=![]() .
.
故答案为:![]() ;
;
(2)如图2,过点C作CE⊥x轴于E,
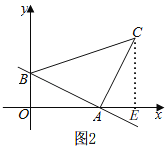
∴∠AEC=∠BOA=90°.
∵∠BAC=90°,
∴∠OAB+∠CAE=90°,
∵∠OAB+∠OBA=90°,
∴∠OBA=∠CAE,
由旋转知,AB=AC,
∴△AOB≌△CEA,
∴AE=OB,CE=OA,
由图2知,点C的纵坐标是点B纵坐标的2倍,
∴OA=2OB,
∴AB2=5OB2,
由(1)知,S△ABC=![]() =
=![]() AB2=
AB2=![]() ×5OB2,
×5OB2,
∴OB=1,
∴OA=2,
∴A(2,0),B(0,1),
∴直线AB的解析式为y=﹣![]() x+1;
x+1;
(3)由(2)知,AB2=5,
∴AB=![]() ,
,
①当0≤m≤![]() 时,如图3,
时,如图3,
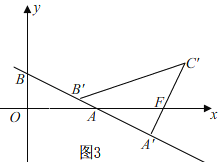
∵∠AOB=∠AA'F,∠OAB=∠A'AF,
∴△AOB∽△AA'F,
∴![]() ,
,
由运动知,AA'=m,∴![]() ,
,
∴A'F=![]() m,
m,
∴S=![]() AA'×A'F=
AA'×A'F=![]() m2,
m2,
②当![]() <m≤2
<m≤2![]() 时,如图4,
时,如图4,
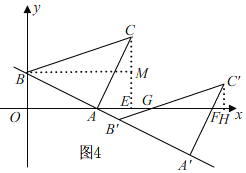
同①的方法得:A'F=![]() m,
m,
∴C'F=![]() ﹣
﹣![]() m,
m,
过点C作CE⊥x轴于E,过点B作BM⊥CE于E,
∴BM=3,CM=1,
易知,△ACE∽△FC'H,
∴![]() ,
,
∴![]() ,
,
∴C'H=![]() .
.
在Rt△FHC'中,FH=![]() C'H=
C'H=![]() ,
,
由平移知,∠C'GF=∠CBM,
∵∠BMC=∠GHC',
∴△BMC∽△GHC',
∴![]() ,
,
∴![]() ,
,
∴GH=![]() ,
,
∴GF=GH﹣FH=![]() ,
,
∴S=S△A'B'C'﹣S△C'FG=![]() ﹣
﹣![]() ×
×![]() ×
×![]() =
=![]() ﹣
﹣![]() (2
(2![]() ﹣m)2,
﹣m)2,
即:S=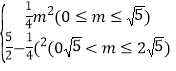 .
.
-
科目: 来源: 题型:
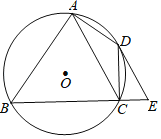
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=8,CE=2时,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
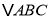 中,
中,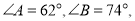 请按要求用尺规作出下列图形(不写作法,但要保留作图痕迹),并填空.
请按要求用尺规作出下列图形(不写作法,但要保留作图痕迹),并填空.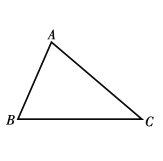
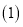 作出
作出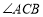 的平分线交
的平分线交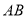 于点
于点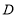 ;
;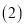 作
作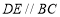 交
交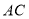 于点
于点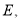 平行依据是_____ __;
平行依据是_____ __;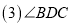 的度数为 .
的度数为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】幻方是一种将数字排在正方形格子中,使每行、每列和每条对角线上的数字和都相等的模型.数学课上,老师在黑板上画出一个幻方如图所示,并设计游戏:一人将一颗能粘在黑板上的磁铁豆随机投入幻方内,另一人猜数,若所猜数字与投出的数字相符,则猜数的人获胜,否则投磁铁豆的人获胜.猜想的方法从以下两种中选一种:
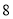
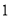
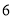
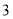
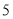

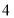
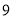
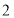
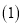 猜“是大于
猜“是大于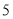 的数”或“不是大于
的数”或“不是大于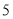 的数”;
的数”;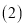 猜“是
猜“是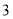 的倍数”或“不是
的倍数”或“不是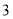 的倍数”;
的倍数”;如果轮到你猜想,那么为了尽可能获胜,你将选择哪--种猜数方法?怎么猜?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小明遇到这样一个问题:
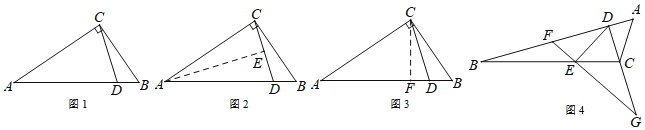
如图1,△ABC中,∠ACB=90°,点D在AB上,且∠BAC=2∠DCB,求证:AC=AD.
小明发现,除了直接用角度计算的方法外,还可以用下面两种方法:
方法1:如图2,作AE平分∠CAB,与CD相交于点E.
方法2:如图3,作∠DCF=∠DCB,与AB相交于点F.
(1)根据阅读材料,任选一种方法,证明AC=AD.
用学过的知识或参考小明的方法,解决下面的问题:
(2)如图4,△ABC中,点D在AB上,点E在BC上,且∠BDE=2∠ABC,点F在BD上,且∠AFE=∠BAC,延长DC、FE,相交于点G,且∠DGF=∠BDE.
①在图中找出与∠DEF相等的角,并加以证明;
②若AB=kDF,猜想线段DE与DB的数量关系,并证明你的猜想.
-
科目: 来源: 题型:
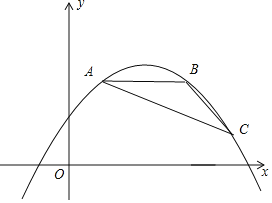
查看答案和解析>>【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣
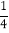 <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】校车安全是近几年社会关注的热点问题,安全隐患主要是超速和超载.某中学九年级数学活动小组进行了测试汽车速度的实验,如图,先在笔直的公路l旁选取一点A,在公路l上确定点B、C,使得AC⊥l,∠BAC=60°,再在AC上确定点D,使得∠BDC=75°,测得AD=40米,已知本路段对校车限速是50千米/时,若测得某校车从B到C匀速行驶用时10秒,问这辆车在本路段是否超速?请说明理由(参考数据:
 =1.41,
=1.41, =1.73)
=1.73)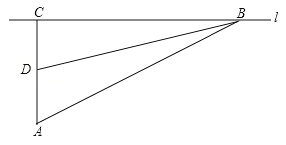
相关试题

