【题目】2011年国家对“酒后驾车”加大了处罚力度,出台了不准酒后驾车的禁令.某记者在一停车场对开车的司机进行了相关的调查,本次调查结果有四种情况:①偶尔喝点酒后开车;②已戒酒或从来不喝酒;③喝酒后不开车或请专业司机代驾;④平时喝酒,但开车当天不喝酒.将这次调查情况整理并绘制了如下尚不完整的统计图,请根据相关信息,解答下列问题.
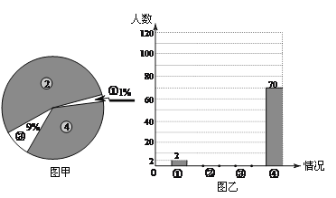
(1)该记者本次一共调查了 _____名司机.
(2)求图甲中④所在扇形的圆心角,并补全图乙.
(3)在本次调查中,记者随机采访其中的一名司机,求他属第②种情况的概率.
(4)请估计开车的10万名司机中,不违反“酒驾”禁令的人数.
参考答案:
【答案】解:(1)2÷1%=200
(2)360°×![]() =126°∴④所在扇形的圆心角为126°
=126°∴④所在扇形的圆心角为126°
200×9%=18(人)
200-18-2-70=110(人)
第②种情况110人,第③种情况18人.
注:补图②110人,③18人
(3)P(第②种情况)=![]()
∴他是第②种情况的概率为![]()
(4)10×(1-1%)=9.9(万人)
即:10万名开车的司机中,不违反“酒驾”禁令的人数为9.9万人
【解析】(1)从扇形图可看出①种情况占1%,从条形图知道有2人,所以可求出总人数;
(2)求出④所占的百分比然后乘以360°就可得到圆心角度数,然后求出其他情况的人,补全条形图;
(3)②种情况的概率为②中调查的人数除以调查的总人数;
(4)10万人数减去第①种情况的人数就是不违反“酒驾“禁令的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】按下列要求画图(不需书写结论)并填空;如右图,
(1)过点Q作QD⊥AB,垂足为D,
(2)过点Q作QE∥AB,交AC于点E,
(3)过点Q作QF⊥直线 AC,垂足为F,
(4)联结A、Q两点,
(5)点Q到直线AC的距离是线段 的长度,
(6)直线QE与直线AB之间的距离是线段 的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】几何探究题
(1)发现:在平面内,若BC=a,AC=b,其中a>b.
当点A在线段BC上时(如图1),线段AB的长取得最小值,最小值为 ;
当点A在线段BC延长线上时(如图2),线段AB的长取得最大值,最大值为 .
(2)应用:点A为线段BC外一动点,如图3,分别以AB、AC为边,作等边△ABD和等边△ACE,连接CD、BE.
①证明:CD=BE;
②若BC=3,AC=1,则线段CD长度的最大值为 .
(3)拓展:如图4,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线AB外一动点,且PA=2,PM=PB,∠BPM=90°.请直接写出线段AM长的最大值及此时点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把
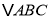 的三边BA、CB和AC分别向外延长一倍,将得到的点
的三边BA、CB和AC分别向外延长一倍,将得到的点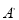 ,
,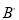 ,
,  顺次连接成△
顺次连接成△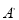
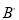
 ,若△ABC的面积是3,则△
,若△ABC的面积是3,则△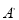
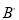
 的面积是( )
的面积是( )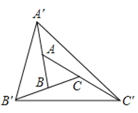
A.15B.18C.21D.24
-
科目: 来源: 题型:
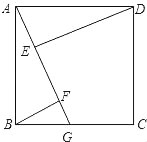
查看答案和解析>>【题目】如图,ABCD是正方形,点G是BC上的任意一点,DE⊥AG于E,BF∥DE,交AG于F.
求证:AF=BF+EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c是△ABC的三边长,且满足a2+2ab=c2+2bc,试判断这个三角形的形状.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BE∥AO,
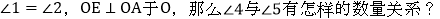
解:因为BE∥AO.(已知)
所以
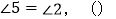
因为
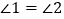 ,(已知 )
,(已知 )所以 .(等量代换)
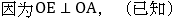
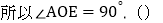
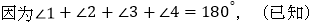
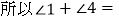 .(等式性质)
.(等式性质)因为 ,(已求)
所以 .(等量代换)
相关试题

