【题目】计算下列各式,且把结果化为只含有正整数指数的形式:
(1)(x﹣2)﹣3(yz﹣1)3 ;(2)a2b3(2a﹣1b)3
(3)(3a3b2c﹣1)﹣2(5ab﹣2c3)2;(4)![]() .
.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() (4)0.
(4)0.
【解析】(1)利用积的乘方运算法则进行化简,得出即可;
(2)利用积的乘方运算法则进行化简,进而利用同底数幂的乘法运算法则得出即可;
(3)利用积的乘方运算法则进行化简,进而利用同底数幂的乘法运算法则得出即可;
(4)利用负整数指数幂的性质以及有理数加减运算法则得出即可.
解:(1)原式=x6y3z﹣3= ![]() ;
;
(2)原式=a2b38a﹣3b3=8a﹣1b6=![]()
(3)原式= ![]() a﹣6b﹣4c225a2b﹣4c6=
a﹣6b﹣4c225a2b﹣4c6= ![]() a﹣4b﹣8c8=
a﹣4b﹣8c8=![]() ;
;
(4)解:原式=1﹣4+3=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x、y的方程组
 .
.(1)当a满足22a+3﹣22a+1=96时,求方程组的解;
(2)当程组的解满足x+y=16时,求a的值;
(3)试说明:不论a取什么实数,x的值始终为正数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:求l+2+22+23+24+…+22013的值.
解:设S=l+2+22+23+24+…+22012+22013,将等式两边同时乘2,
得2S=2+22+23+24+25+…+22013+22014. 将下式减去上式,得2S﹣S=22014-1
即S=22014-1,
即1+2+22+23+24+…+22013=22014-1
仿照此法计算:(1)1+3+32+33+…+3100;(2)1+
 +
+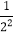 +
+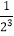 +…+
+…+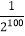 ,
, -
科目: 来源: 题型:
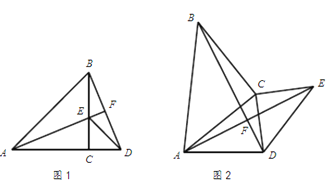
查看答案和解析>>【题目】在△ABC和△DEC中,AC=BC,DC=EC,∠ACB=∠ECD=90°.
(1)如图1,当点A、C、D在同一条直线上时,AC=12,EC=5,
①求证:AF⊥BD; ②求AF的长度;
(2)如图2,当点A、C、D不在同一条直线上时,求证:AF⊥BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是AB上一点,DF交AC于点E,AE=EC,DE=EF,则下列说法中:①∠ADE=∠EFC;②∠ADE+∠ECF+∠FEC=180°;③∠B+∠BCF=180°;④S△ABC=S四边形DBCF.正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂设计了一款工艺品,每件成本
 元,为了合理定价,现投放市场进行试销.据市场调查,销售单价是
元,为了合理定价,现投放市场进行试销.据市场调查,销售单价是 元时,每天的销售量是
元时,每天的销售量是 件,若销售单价每降低
件,若销售单价每降低 元,每天就可多售出
元,每天就可多售出 件,但要求销售单价不得低于
件,但要求销售单价不得低于 元.如果降价后销售这款工艺品每天能盈利
元.如果降价后销售这款工艺品每天能盈利 元,那么此时销售单价为多少元?
元,那么此时销售单价为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】云南地区地震发生后,市政府筹集了必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)

(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,市政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能求出这三种车型分别有多少辆吗?此时的运费又是多少元?
相关试题

