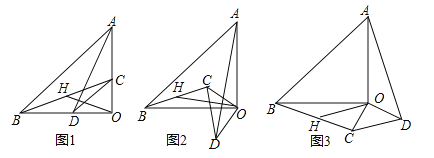
【题目】(2017黑龙江省龙东地区)已知:△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°.连接AD,BC,点H为BC中点,连接OH.
(1)如图1所示,易证:OH=![]() AD且OH⊥AD(不需证明)
AD且OH⊥AD(不需证明)
(2)将△COD绕点O旋转到图2,图3所示位置时,线段OH与AD又有怎样的关系,并选择一个图形证明你的结论.
参考答案:
【答案】(1)证明见解析;(2)图2,图3的结论都相同:OH=![]() AD,OH⊥AD.
AD,OH⊥AD.
【解析】试题(1)只要证明△AOD≌△BOC,即可解决问题;
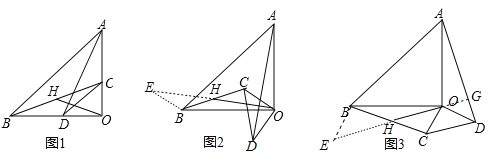
(2)①如图2中,结论:OH=![]() AD,OH⊥AD.延长OH到E,使得HE=OH,连接BE,由△BEO≌△ODA即可解决问题;
AD,OH⊥AD.延长OH到E,使得HE=OH,连接BE,由△BEO≌△ODA即可解决问题;
②如图3中,结论不变.延长OH到E,使得HE=OH,连接BE,延长EO交AD于G.由△BEO≌△ODA即可解决问题;
试题解析:(1)证明:如图1中,∵△OAB与△OCD为等腰直角三角形,∠AOB=∠COD=90°,∴OC=OD,OA=OB,在△AOD与△BOC中,∵OA=OB,∠AOD=∠BOC,OD=OC,∴△AOD≌△BOC(SAS),∴∠ADO=∠BCO,∠OAD=∠OBC,∵点H为线段BC的中点,∴OH=HB,∴∠OBH=∠HOB=∠OAD,又∵∠OAD+∠ADO=90°,∴∠ADO+∠BOH=90°,∴OH⊥AD;
(2)解:①结论:OH=![]() AD,OH⊥AD,如图2中,延长OH到E,使得HE=OH,连接BE,易证△BEO≌△ODA,∴OE=AD,∴OH=
AD,OH⊥AD,如图2中,延长OH到E,使得HE=OH,连接BE,易证△BEO≌△ODA,∴OE=AD,∴OH=![]() OE=
OE=![]() AD.由△BEO≌△ODA,知∠EOB=∠DAO,∴∠DAO+∠AOH=∠EOB+∠AOH=90°,∴OH⊥AD.
AD.由△BEO≌△ODA,知∠EOB=∠DAO,∴∠DAO+∠AOH=∠EOB+∠AOH=90°,∴OH⊥AD.
②如图3中,结论不变.延长OH到E,使得HE=OH,连接BE,延长EO交AD于G.
易证△BEO≌△ODA,∴OE=AD,∴OH=![]() OE=
OE=![]() AD.
AD.
由△BEO≌△ODA,知∠EOB=∠DAO,∴∠DAO+∠AOF=∠EOB+∠AOG=90°,∴∠AGO=90°,∴OH⊥AD.
-
科目: 来源: 题型:
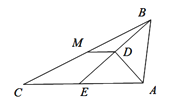
查看答案和解析>>【题目】如图,在△ABC中,点E是边AC上一点,线段BE垂直于∠BAC的平分线于点D,点M为边BC的中点,连接DM.
(1)求证: DM=
 CE;
CE; (2)若AD=6,BD=8,DM=2,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 分别平分
分别平分 和
和 ,交
,交 于点
于点 ,线段
,线段 相交于点M.
相交于点M.(1)求证:
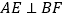 ;
;(2)若
 ,则
,则 的值是__________.
的值是__________. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
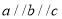 ,
,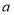 与
与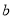 之间的距离为3,
之间的距离为3, 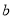 与
与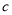 之间的距离为6,
之间的距离为6, 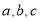 分别等边三角形
分别等边三角形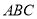 的三个顶点,则此三角形的边长为__________.
的三个顶点,则此三角形的边长为__________.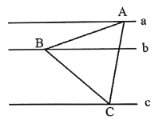
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A. 7.5平方千米 B. 15平方千米 C. 75平方千米 D. 750平方千米
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:A=2a2+3ab-2a-1,B=-a2+ab+1.
(1)若 |a+1| b- 22 0 ,求4A-(3A-2B)的值;
(2)若(1)中代数式的值与a的取值无关,求b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…,根据以上操作,若要得到2011个小正方形,则需要操作的次数是( )

A. 669 B. 670 C. 671 D. 672
相关试题

