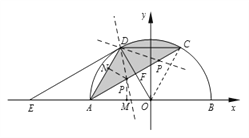
【题目】如图, ![]() 为
为![]() 的直径,
的直径, ![]() 为弦
为弦![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ∥
∥![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,
, ![]() .
.
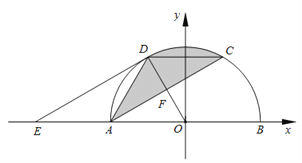
(1)求证: ![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() 时,
时,
①求图中阴影部分的面积;
②以![]() 为原点,
为原点, ![]() 所在的直线为
所在的直线为![]() 轴,直径
轴,直径![]() 的垂直平分线为
的垂直平分线为![]() 轴,建立如图所示的平面直角坐标系,试在线段
轴,建立如图所示的平面直角坐标系,试在线段![]() 上求一点
上求一点![]() ,使得直线
,使得直线![]() 把阴影部分的面积分成
把阴影部分的面积分成![]() 的两部分.
的两部分.
参考答案:
【答案】(1)证明见解析;(2) ①![]() ②
②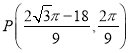 或
或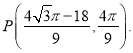
【解析】试题分析:(1)、连接OC,根据等腰三角形的三线合一定理得出OD⊥AC,根据平行线的性质得出OD⊥DE,从而得出切线;(2)、首先得出△AOD为等边三角形,然后根据题意得出△ACD和△OCD的面积相等,从而得出阴影部分的面积等于扇形OCD的面积,然后根据扇形的面积计算法则得出答案;(3)、根据题意得出直线AC的解析式,过点P分别作PM⊥x轴,PN⊥AD,垂足分别为M,N,设设![]() 根据面积分成1:2两部分得出△APD的面积等于阴影部分面积的
根据面积分成1:2两部分得出△APD的面积等于阴影部分面积的![]() 或
或![]() 列出方程,求出x的值,得出点P的坐标.
列出方程,求出x的值,得出点P的坐标.
试题解析:(1)、连结![]() ∵
∵![]()
![]() 为
为![]() 的中点 ∴
的中点 ∴![]() 又∵
又∵![]()
∴![]() ∴
∴![]() 是⊙O的切线
是⊙O的切线
(2)、①由(1)得![]() ∴
∴![]() ∴
∴![]() ∴
∴![]()
∴![]() ∴
∴![]() 是等边三角形 ∴
是等边三角形 ∴![]()
∴![]() 又∵
又∵![]() ∴
∴![]()
∴![]() ∴
∴![]()
∴![]() ∴
∴![]() ∵
∵![]()
∴![]() ∴
∴![]()
②由已知得: ![]() ∴直线
∴直线![]() 的表达式为
的表达式为![]()
过点P分别作![]() 轴,
轴, ![]() 垂足分别为
垂足分别为![]() ,
, ![]() , 由①得
, 由①得![]() 平分
平分![]()
∴![]() 设
设![]()
![]() ∵直线
∵直线![]() 把阴影部分的面积分成
把阴影部分的面积分成![]() 的两部分
的两部分
若![]() 即
即![]()
解得: ![]() ,此时
,此时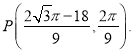
若![]() 同理可求得
同理可求得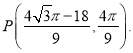
综上所述:满足条件的点P的坐标为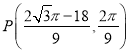 和
和
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:化简:5(3a2b-ab2)—3(ab2+3a2b)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DE,则∠CDF等于( )

A.60°
B.65°
C.70°
D.80° -
科目: 来源: 题型:
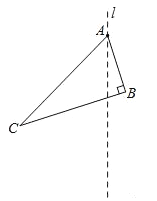
查看答案和解析>>【题目】如图,已知Rt△ABC中,∠ABC=90°,经过点A的直线l与BC交于点F.
(1)请作出△ABC关于直线l轴对称的△ADE(A、B、C的对应点分别是A、D、E)
(2)连接CD,EB,在不添加其它辅助线的情况下,请你找出图中的一对全等三角形: ≌ ;
(3)证明(2)中的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校在“校园读书节”活动中,购买甲、乙两种图书共100本作为奖品,已知乙种图书的单价比甲种图书的单价高出50%.同样用360元购买乙种图书比购买甲种图书少4本.
(1)求甲、乙两种图书的单价各是多少元;
(2)如果购买图书的总费用不超过3500元,那么乙种图书最多能买多少本?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是方程x 2+3x-6=0的根,则代数式3a 2+9a+12的值为________
-
科目: 来源: 题型:
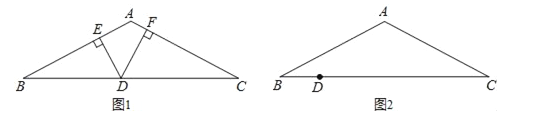
查看答案和解析>>【题目】如图1,在△ABC中,AB=AC,D为BC边上一点,DE⊥AB于E,DF⊥AC于F.
作图:
(1)请作出AC边上的高BG.
探究:
(2)请你通过观察、测量找到DE、DF、BG之间的数量关系: ;
(3)为了说明DE、DF、BG之间的数量关系,小嘉是这样做的:
连接AD,则S△ADC= ,S△ABD= ,∴S△ABC= ,S△ABC还可以表示为 …
请你帮小嘉完成上述填空:
拓展:
(4)如图2,当D在如图2的位置时,上面DE、DF、BG之间的数量关系是否仍然成立?并说明理由
相关试题

