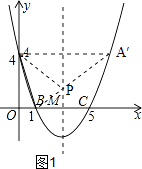
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:根据已知条件可设抛物线的解析式为y=a(x﹣1)(x﹣5),
把点A(0,4)代入上式得:a= ![]() ,
,
∴y= ![]() (x﹣1)(x﹣5)=
(x﹣1)(x﹣5)= ![]() x2﹣
x2﹣ ![]() x+4=
x+4= ![]() (x﹣3)2﹣
(x﹣3)2﹣ ![]() ,
,
∴抛物线的对称轴是:x=3
(2)
解:P点坐标为(3, ![]() ).
).
理由如下:
∵点A(0,4),抛物线的对称轴是x=3,
∴点A关于对称轴的对称点A′的坐标为(6,4)
如图1,连接BA′交对称轴于点P,连接AP,此时△PAB的周长最小.
设直线BA′的解析式为y=kx+b,
把A′(6,4),B(1,0)代入得 ![]() ,
,
解得  ,
,
∴y= ![]() x﹣
x﹣ ![]() ,
,
∵点P的横坐标为3,
∴y= ![]() ×3﹣
×3﹣ ![]() =
= ![]() ,
,
∴P(3, ![]() ).
).
(3)
解:在直线AC的下方的抛物线上存在点N,使△NAC面积最大.
设N点的横坐标为t,此时点N(t, ![]() t2﹣
t2﹣ ![]() t+4)(0<t<5),
t+4)(0<t<5),
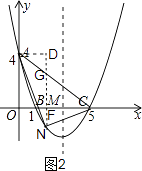
如图2,过点N作NG∥y轴交AC于G;作AD⊥NG于D,
由点A(0,4)和点C(5,0)可求出直线AC的解析式为:y=﹣ ![]() x+4,
x+4,
把x=t代入得:y=﹣ ![]() t+4,则G(t,﹣
t+4,则G(t,﹣ ![]() t+4),
t+4),
此时:NG=﹣ ![]() t+4﹣(
t+4﹣( ![]() t2﹣
t2﹣ ![]() t+4)=﹣
t+4)=﹣ ![]() t2+4t,
t2+4t,
∵AD+CF=CO=5,
∴S△ACN=S△ANG+S△CGN= ![]() AD×NG+
AD×NG+ ![]() NG×CF=
NG×CF= ![]() NGOC=
NGOC= ![]() ×(﹣
×(﹣ ![]() t2+4t)×5=﹣2t2+10t=﹣2(t﹣
t2+4t)×5=﹣2t2+10t=﹣2(t﹣ ![]() )2+
)2+ ![]() ,
,
∴当t= ![]() 时,△CAN面积的最大值为
时,△CAN面积的最大值为 ![]() ,
,
由t= ![]() ,得:y=
,得:y= ![]() t2﹣
t2﹣ ![]() t+4=﹣3,
t+4=﹣3,
∴N( ![]() ,﹣3)
,﹣3)
【解析】(1)抛物线经过点A(0,4),B(1,0),C(5,0),可利用两点式法设抛物线的解析式为y=a(x﹣1)(x﹣5),代入A(0,4)即可求得函数的解析式,则可求得抛物线的对称轴;(2)点A关于对称轴的对称点A′的坐标为(6,4),连接BA′交对称轴于点P,连接AP,此时△PAB的周长最小,可求出直线BA′的解析式,即可得出点P的坐标.(3)在直线AC的下方的抛物线上存在点N,使△NAC面积最大.设N点的横坐标为t,此时点N(t, ![]() t2﹣
t2﹣ ![]() t+4)(0<t<5),再求得直线AC的解析式,即可求得NG的长与△ACN的面积,由二次函数最大值的问题即可求得答案.
t+4)(0<t<5),再求得直线AC的解析式,即可求得NG的长与△ACN的面积,由二次函数最大值的问题即可求得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,正比例函数
中,正比例函数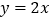 与反比例函数
与反比例函数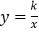 的图象交于A,B两点,A点的横坐标为2,AC⊥x轴于点C,连接BC.
的图象交于A,B两点,A点的横坐标为2,AC⊥x轴于点C,连接BC.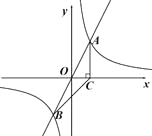
(1)求反比例函数的解析式;
(2)若点P是反比例函数
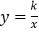 图象上的一点,且满足△OPC与△ABC的面积相等,请直接写出点P的坐标.
图象上的一点,且满足△OPC与△ABC的面积相等,请直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的边长为48cm,∠A=60°,动点P从点A出发,沿着线路AB﹣BD做匀速运动,动点Q从点D同时出发,沿着线路DC﹣CB﹣BA做匀速运动.

(1)求BD的长;
(2)已知动点P、Q运动的速度分别为8cm/s、10cm/s.经过12秒后,P、Q分别到达M、N两点,试判断△AMN的形状,并说明理由,同时求出△AMN的面积;
(3)设问题(2)中的动点P、Q分别从M、N同时沿原路返回,动点P的速度不变,动点Q的速度改变为a cm/s,经过3秒后,P、Q分别到达E、F两点,若△BEF为直角三角形,试求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点A(a,0),B(0,b),且a、b满足
 =0, □ABCD的边AD与y轴交于点E(0,2),且E为AD中点,双曲线
=0, □ABCD的边AD与y轴交于点E(0,2),且E为AD中点,双曲线 经过C、D两点.
经过C、D两点. (1)求k的值;
(2)点P在双曲线
 上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;(3)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时,
 的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司员工分别住在A、B、C、D四个住宅区,A区有20人,B区有15人,C区有5人,D区有30人,四个区在同一条直线上,位置如图所示.该公司的接送车打算在此间设立一个停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠点的位置应设置在( )

A. D区 B. A区 C. AB两区之间 D. BC两区之间
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B、C在同一直线上,H为AC的中点,M为AB的中点,N为BC的中点,则下列说法:①MN=HC;②MH=
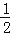 (AH﹣HB);③MN=
(AH﹣HB);③MN=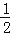 (AC+HB);④HN=
(AC+HB);④HN=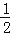 (HC+HB),其中正确的是( )
(HC+HB),其中正确的是( )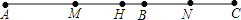
A.①② B.①②④ C.②③④ D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,线段AB和射线BM交于点B.
(1)利用尺规完成以下作图,并保留作图痕迹(不写作法)
①在射线BM上作一点C,使AC=AB;
②作∠ABM 的角平分线交AC于D点;
③在射线CM上作一点E,使CE=CD,连接DE.

(2)在(1)所作的图形中,猜想线段BD与DE的数量关系,并证明之.
相关试题

